题目内容
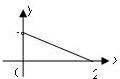 f(x)为定义在区间(-2,2)的奇函数,它在区间(0,2)上的图象为如图所示的一条线段,则不等式f(x)-f(-x)>x的解集为
f(x)为定义在区间(-2,2)的奇函数,它在区间(0,2)上的图象为如图所示的一条线段,则不等式f(x)-f(-x)>x的解集为(-2,-1)∪(0,1)
(-2,-1)∪(0,1)
.分析:f(x)-f(-x)>x可化为f(x)>
x,由奇函数的性质作出f(x)的图象,再作出y=
x的图象,根据图象求出f(x),y=f(x)与y=
x的交点,结合图象即可求出解集.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:因为f(x)为奇函数,所以f(x)-f(-x)>x可化为f(x)+f(x)>x,即f(x)>
x,
由奇函数的图象关于原点对称,可作出函数f(x)的图象及y=
x的图象,如图所示:
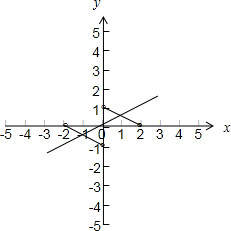
由图象可求得f(x)=
,
由
解得x=1,由
解得x=-1,
结合图象知f(x)>
x,即(x)-f(-x)>x的解集为(-2,-1)∪(0,1).
故答案为:(-2,-1)∪(0,1).
| 1 |
| 2 |
由奇函数的图象关于原点对称,可作出函数f(x)的图象及y=
| 1 |
| 2 |
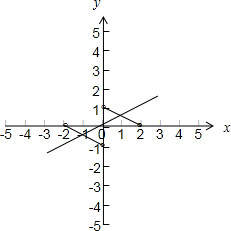
由图象可求得f(x)=
|
由
|
|
结合图象知f(x)>
| 1 |
| 2 |
故答案为:(-2,-1)∪(0,1).
点评:本题考查函数奇偶性的应用,属基础题,注意数形结合思想在解不等式中的应用.

练习册系列答案
相关题目
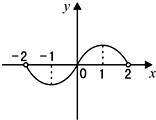 f(x)为定义在区间(-2,2)上的连续函数,它的导函数f'(x)的图象如图,则下列结论正确的是( )
f(x)为定义在区间(-2,2)上的连续函数,它的导函数f'(x)的图象如图,则下列结论正确的是( ) (2010•孝感模拟)f(x)为定义在区间[-2,2]上的连续函数,它的导函数f(x)的图象如图,则下面结论正确的是( )
(2010•孝感模拟)f(x)为定义在区间[-2,2]上的连续函数,它的导函数f(x)的图象如图,则下面结论正确的是( )