Question

一个球与正四面体的六条棱都相切，若正四面体的棱长为a，则这个球的体积是_。

 

Answer 1

【答案】

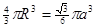
【解析】

试题分析：将正四面体ABCD“嵌入”到正方体中，使正四面体的六条棱分别是正方体六个面的面对角线（如图），则球O与正四面体的六条棱都相切等价于球O与正方体的六个

面都相切。易知正方体棱长为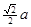，所以球半径为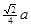，故球的体积为 。

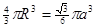考点：本题主要考查正四面体及球的几何特征、球体积计算。

点评：此题将正四面体补成正方体进行研究，这种割、补、拼凑的思想，是解答立体几何问题的重要方法。