题目内容
已知函数f(x)=-| 2 |
| 2 |
| ||
| 2 |
(1)求f(x)的单调增区间
(2)在直角坐标系中画出函数y=f(x)在区间[0,π]上的图象.
分析:(1)利用倍角公式和两角差的正弦公式,对解析式进行化简,再由正弦函数的增区间以及2x-
看出一个整体,求出原函数的增区间;
(2)利用五点作图法和正弦函数的图象,在坐标系中画出函数图象.
| 3π |
| 4 |
(2)利用五点作图法和正弦函数的图象,在坐标系中画出函数图象.
解答:解:(1)f(x)=-
sin2x-
•
+
=-
sin2x-
cos2x=sin(2x-
),
∴-
+2kπ≤2x-
≤
+2kπ,k∈Z,
∴函数y=f(x)的单调增区间为[
+kπ,
+kπ],k∈Z
(2)由(1)知,f(x)=sin(2x-
),
利用五点作图法画出函数在区间[0,π]上的图象:
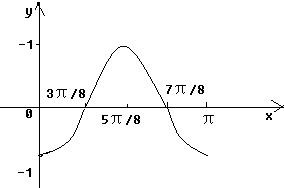
| ||
| 2 |
| 2 |
| 1+cos2x |
| 2 |
| ||
| 2 |
=-
| ||
| 2 |
| ||
| 2 |
| 3π |
| 4 |
∴-
| π |
| 2 |
| 3π |
| 4 |
| π |
| 2 |
∴函数y=f(x)的单调增区间为[
| π |
| 8 |
| 5π |
| 8 |
(2)由(1)知,f(x)=sin(2x-
| 3π |
| 4 |
利用五点作图法画出函数在区间[0,π]上的图象:

点评:本题考查了正弦函数的单调性和图象的应用,主要根据三角恒等变换的公式对解析式进行化简后,利用整体思想和正弦函数的性质进行求解,还考查了五点作图能力.

练习册系列答案
相关题目
 已知函数f(x)=
已知函数f(x)=
|
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、[
|