题目内容
已知集合A为函数f(x)=lg(1+x)-lg(1-x)的定义域,集合B={x|1-a2-2ax-x2≥0}.(I)若A∩B={x|
 ≤x<1},求a的值;
≤x<1},求a的值;(II)求证a≥2是A∩B=φ的充分不必要条件.
【答案】分析:(I)根据对数函数的性质可以求出f(x)的定义域,得到集合A,利用十字相乘法,求出集合B,再根据A∩B={x| ≤x<1},求出a值;
≤x<1},求出a值;
(II)由(I)知:B=[-1-a,1-a],已知a≥2,根基交集的定义可以判断集合A与B的关系,利用特殊值法证明A∩B=∅推不出a≥2,从而进行证明;
解答:解:(I)要使函数f(x)=lg(1+x)-lg(1-x)有意义,可得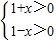
即-1<x<1,∴A={x|-1<x<1},
由1-a2-2ax-x2≥0得x2+2ax+a2-1≤0即(x+a-1)(x+a+1)≤0,
∴-1-a≤x≤1-a
从而B={x|-1-a≤x≤1-a},
∵A∩B={x| ≤x<1},
≤x<1},
∴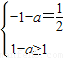 ,解得a=-
,解得a=- ;
;
(II)由(I)知:B=[-1-a,1-a]
当a≥2时,1-a≤-1,
由A=(-1,1),B=[-1-a,1-a],有A∩B=∅,
反之,若A∩B=∅,可取-a-1=2,解得a=-3,a<2,
所以a≥2是A∩B=∅的充分不必要条件;
点评:此题主要考查集合间的参数关系,以及对数函数的性质,注意理解集合空集的含义,第二问涉及充分不必要条件的定义,利用特殊值法进行证明会比较简单;
 ≤x<1},求出a值;
≤x<1},求出a值;(II)由(I)知:B=[-1-a,1-a],已知a≥2,根基交集的定义可以判断集合A与B的关系,利用特殊值法证明A∩B=∅推不出a≥2,从而进行证明;
解答:解:(I)要使函数f(x)=lg(1+x)-lg(1-x)有意义,可得
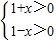
即-1<x<1,∴A={x|-1<x<1},
由1-a2-2ax-x2≥0得x2+2ax+a2-1≤0即(x+a-1)(x+a+1)≤0,
∴-1-a≤x≤1-a
从而B={x|-1-a≤x≤1-a},
∵A∩B={x|
 ≤x<1},
≤x<1},∴
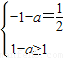 ,解得a=-
,解得a=- ;
;(II)由(I)知:B=[-1-a,1-a]
当a≥2时,1-a≤-1,
由A=(-1,1),B=[-1-a,1-a],有A∩B=∅,
反之,若A∩B=∅,可取-a-1=2,解得a=-3,a<2,
所以a≥2是A∩B=∅的充分不必要条件;
点评:此题主要考查集合间的参数关系,以及对数函数的性质,注意理解集合空集的含义,第二问涉及充分不必要条件的定义,利用特殊值法进行证明会比较简单;

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案
相关题目
 ≤x<1},求a的值;
≤x<1},求a的值;