题目内容
面积为S的矩形中，其周长的最小值为 ．
【答案】分析：将矩形的面积用矩形的长为x，宽为y表示，将周长l=2（x+y）表示，利用基本不等式求出最小值．
解答：解：设矩形的长为x，宽为y，
则S=xy，
周长l=2（x+y）≥4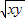
=
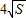
当且仅当x=y=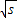
时，l最小为 
故答案为 4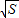
．
点评：利用基本不等式求函数的最值时，一定注意基本不等式使用的条件：一正、二定、三相等．
解答：解：设矩形的长为x，宽为y，
则S=xy，
周长l=2（x+y）≥4
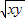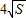
=当且仅当x=y=
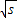时，l最小为 故答案为 4
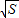．点评：利用基本不等式求函数的最值时，一定注意基本不等式使用的条件：一正、二定、三相等．
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目