题目内容
设函数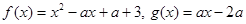 ,若不存在
,若不存在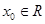 ,使得
,使得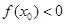 与
与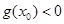 同时成立,则实数
同时成立,则实数 的取值范围是 .
的取值范围是 .
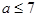
解析试题分析: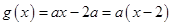 过定点
过定点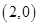 ,当
,当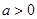 时由
时由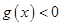 得
得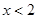 ,此时
,此时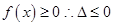 或
或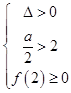 解得
解得 ,当
,当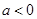 时由
时由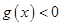 得
得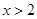 ,此时
,此时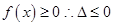 或
或 解得
解得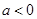 ,当
,当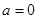 时
时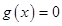 ,不满足
,不满足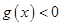 ,综上可知
,综上可知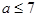
考点:函数性质
点评:求解本题的入手点在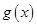 过定点
过定点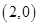 ,结合
,结合 的函数图像分情况讨论转化为二次方程根
的函数图像分情况讨论转化为二次方程根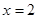 的分布问题,本题有一定难度
的分布问题,本题有一定难度

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
设函数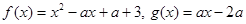 ,若不存在
,若不存在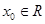 ,使得
,使得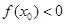 与
与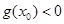 同时成立,则实数
同时成立,则实数 的取值范围是 .
的取值范围是 .
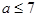
解析试题分析: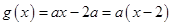 过定点
过定点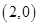 ,当
,当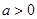 时由
时由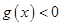 得
得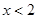 ,此时
,此时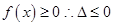 或
或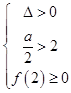 解得
解得 ,当
,当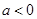 时由
时由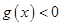 得
得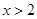 ,此时
,此时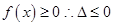 或
或 解得
解得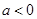 ,当
,当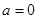 时
时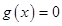 ,不满足
,不满足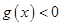 ,综上可知
,综上可知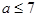
考点:函数性质
点评:求解本题的入手点在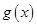 过定点
过定点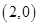 ,结合
,结合 的函数图像分情况讨论转化为二次方程根
的函数图像分情况讨论转化为二次方程根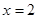 的分布问题,本题有一定难度
的分布问题,本题有一定难度

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案