题目内容
已知点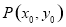 在直线
在直线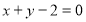 上,若圆
上,若圆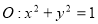 (
(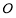 为坐标原点)上存在点
为坐标原点)上存在点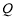 使得
使得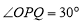 ,则
,则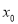 的取值范围为 .
的取值范围为 .
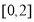
【解析】
试题分析:由已知条件得圆O与直线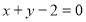 相离,当
相离,当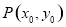 在
在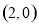 且满足
且满足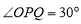 时,
时,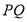 是圆O的切线;当
是圆O的切线;当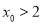 且满足
且满足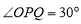 时,
时,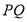 与圆O相离,即满足条件的点
与圆O相离,即满足条件的点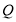 不存在;同理当
不存在;同理当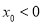 时点
时点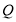 亦不存在;综上可知
亦不存在;综上可知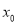 的取值范围为
的取值范围为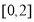 .
.
考点:直线与圆的位置关系,圆的方程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
已知点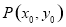 在直线
在直线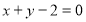 上,若圆
上,若圆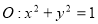 (
(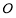 为坐标原点)上存在点
为坐标原点)上存在点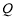 使得
使得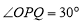 ,则
,则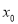 的取值范围为 .
的取值范围为 .
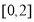
【解析】
试题分析:由已知条件得圆O与直线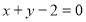 相离,当
相离,当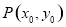 在
在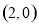 且满足
且满足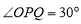 时,
时,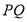 是圆O的切线;当
是圆O的切线;当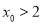 且满足
且满足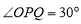 时,
时,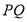 与圆O相离,即满足条件的点
与圆O相离,即满足条件的点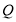 不存在;同理当
不存在;同理当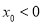 时点
时点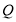 亦不存在;综上可知
亦不存在;综上可知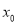 的取值范围为
的取值范围为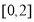 .
.
考点:直线与圆的位置关系,圆的方程.

 阅读快车系列答案
阅读快车系列答案