题目内容
下列说法正确的是
- A.命题“存在x∈R,x2+1>3x”的否定是“对任意x∈R,x2+1<3x”
- B.在空间,m、n是两条不重合的直线,α、β是两个不重合的平面,若α⊥β,α∩β=n,m⊥n,则m⊥β
- C.若函数f(x)=ax+2a-1在[-1,1]上有零点,则实数a的取值范围是(
 ,1)
,1) - D.用最小二乘法求得的线性回归方程
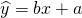 一定过点
一定过点
D
分析:求命题的否定形式,因为命题的否定形式只对结果否定,显然A不正确,对于B因为m并不一定属于α,根据线面垂直的关系定理,不能得到那么m⊥β,即B错误.对于C根据函数的零点的判定定理可以看出不正确,根据线性回归直线一定过样本中心点,知D正确.
解答:A一个是求命题的否定形式,因为命题的否定形式只对结果否定,显然A不正确,
对于B因为m并不一定属于α,根据线面垂直的关系定理,不能得到那么m⊥β,即B错误.
对于C根据函数的零点的判定定理可以看出a的范围不正确
根据线性回归直线一定过样本中心点,知D正确.
故选D.
点评:此题主要考查三角函数的图象变换及空间线面位置关系的判定问题,其中涉及到命题的否定形式和否命题的求法,对于这两个概念是易混淆的地方,希望同学们注意区分.
分析:求命题的否定形式,因为命题的否定形式只对结果否定,显然A不正确,对于B因为m并不一定属于α,根据线面垂直的关系定理,不能得到那么m⊥β,即B错误.对于C根据函数的零点的判定定理可以看出不正确,根据线性回归直线一定过样本中心点,知D正确.
解答:A一个是求命题的否定形式,因为命题的否定形式只对结果否定,显然A不正确,
对于B因为m并不一定属于α,根据线面垂直的关系定理,不能得到那么m⊥β,即B错误.
对于C根据函数的零点的判定定理可以看出a的范围不正确
根据线性回归直线一定过样本中心点,知D正确.
故选D.
点评:此题主要考查三角函数的图象变换及空间线面位置关系的判定问题,其中涉及到命题的否定形式和否命题的求法,对于这两个概念是易混淆的地方,希望同学们注意区分.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,则下列说法正确的是( )
,则下列说法正确的是( ) 有且只有一个零点
B.
有且只有一个零点
B. ,
, ,则下列说法正确的是( )
,则下列说法正确的是( )
 ,乙比甲成绩稳定,应该选乙参加比赛
,乙比甲成绩稳定,应该选乙参加比赛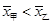 ,甲比乙成绩稳定,应该选甲参加比赛
,甲比乙成绩稳定,应该选甲参加比赛 :函数
:函数 (
( 且
且 )的图像恒过点
)的图像恒过点 ;
; :函数
:函数 有两个零点.
有两个零点.  为假命题 D.
为假命题 D. 为真命题
为真命题 的导函数
的导函数 的图象如上图所示,则下列说法正确的是 ( )
的图象如上图所示,则下列说法正确的是 ( ) 内单调递减 B、函数
内单调递减 B、函数 内单调递增
内单调递增 处取极大值 D、函数
处取极大值 D、函数 处取极小值
处取极小值