题目内容
设f(k)是满足不等式log2x+log2(3×2k-1-x)≥2k-1(k∈N+)的自然数x的个数.
(1)求f(k)的解析式;
(2)记Sn=f(1)+f(2)+…+f(n),求Sn的解析式;
(3)令Pn=n2+n-1(n∈N+),试比较Sn与Pn的大小.
答案:
解析:
解析:
|
解:(1)由已知不等式可得 (2)Sn=f(1)+f(2)+…+f(n) =20+21+…+2n-1+n =2n+n-1. (3)Sn-Pn=2n-n2. 当n=1时,21-12>0;当n=2时,22-22=0; 当n=3时,23-32<0;当n=4时,24-42=0; 当n=5时,25-52>0;当n=6时,26-62>0. 猜想:当n≥5时,Sn>Pn. 下面用数学归纳法证明: ①当n=5时,Sn>Pn,上面已证; ②假设n=k时,Sk>Pk,即2k>k2, 则n=k+1时, ∵Sk-Pk+1=2k+1-(k-1)2>2k2-(k+1)2=(k-1)2-2, 当k≥5时,(k-1)2-2>0,∴Sk+1>Pk+1. 故当n≥5时,总有Sn>Pn成立. 综上可知:当n=1或n≥5时,有Sn>Pn; 当n=2或n=4时,Sn=Pn; 当n=3时,Sn<Pn. |

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
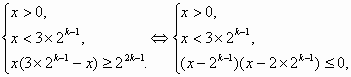
 是递增闭函数,则实数k的取值范围是( )
是递增闭函数,则实数k的取值范围是( )