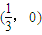题目内容
把函数y=lg(3x)的图象按向量 平移,得到函数
平移,得到函数 为( )
为( )A.(-1,lg3)
B.(1,-lg3)
C.(-1,-lg3)
D.

【答案】分析:先利用图象的平移变换判断出由函数y=lg(3x)的图象向左移一个单位向下移lg3个单位得到函数y=lg(x+1)的图象得到向量的坐标.
解答:解:函数y=lg(3x)=lg3+lgx的图象向左移一个单位得到y=lg(x+1)+lg3
再向下移lg3个单位得到函数y=lg(x+1)-lg3=lg(x+1)
所以
故选C.
点评:本题考查函数图象的变化,只需将原函数式化简,然后遵循相应的变化法则既可.
解答:解:函数y=lg(3x)=lg3+lgx的图象向左移一个单位得到y=lg(x+1)+lg3
再向下移lg3个单位得到函数y=lg(x+1)-lg3=lg(x+1)
所以

故选C.
点评:本题考查函数图象的变化,只需将原函数式化简,然后遵循相应的变化法则既可.

练习册系列答案
相关题目
把函数y=lg(3x)的图象按向量
平移,得到函数y=lg(x+1)的图象,则
为( )
| a |
| a |
| A、(-1,lg3) | ||
| B、(1,-lg3) | ||
| C、(-1,-lg3) | ||
D、(
|
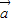 平移,得到函数
平移,得到函数 为( )
为( )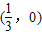
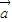 平移,得到函数
平移,得到函数 为( )
为( )