题目内容
已知Q为抛物线(y+1)2=8(x-2)上的任一点,以Q为圆心作与y轴相切的圆,这些圆必过定点( )A.(2,-1) B.(4,-1) C.(6,-1) D.(8,-1)
B
解析：设Q点坐标为(a,b),则(b+1)2=8(a-2),
∴a=
b2+
b+
.
设圆上任一点M坐标为(x,y),则|MQ|=a.
∴(x-a)2+(y-b)2=a2,
即x2+y2-2ax-2by+b2=0.将a=
b2+
b+
代入得(x2+y2-
x)+b2(1-
x)-b(2y+
x)=0.
令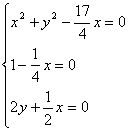
∴定点为(4,-1).
练习册系列答案
相关题目