题目内容
命题“?x∈R,|x-2|+|x-4|≤3”的否定是
?x∈R,|x-2|+|x-4|>3
?x∈R,|x-2|+|x-4|>3
.分析:由题意,本题所给命题是一个特称命题,其否定是一个全称命题,按规则写出其否定即可.
解答:解:由于命题“?x∈R,|x-2|+|x-4|≤3,此命题是一个特称命题,
∴它的否定是“?x∈R,|x-2|+|x-4|>3”
故答案为:?x∈R,|x-2|+|x-4|>3.
∴它的否定是“?x∈R,|x-2|+|x-4|>3”
故答案为:?x∈R,|x-2|+|x-4|>3.
点评:本题考查特称命题的否定,解题的关键是理解特称命题的否定是一个全称命题,本题的易错点是忘记把存在存在称量词改为全称量词,对于特殊命题的否定的书写规则要熟记.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
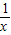 是奇函数”的证明不是综合法的是( )
是奇函数”的证明不是综合法的是( )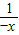 =-(x+
=-(x+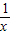 )=-f(x),∴f(x)是奇函数
)=-f(x),∴f(x)是奇函数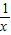 +(-x)+(-
+(-x)+(-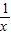 )=0,∴f(x)=-f(-x),∴f(x)是奇函数
)=0,∴f(x)=-f(-x),∴f(x)是奇函数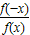 =
=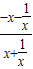 =-1,∴f(-x)=-f(x),∴f(x)是奇函数
=-1,∴f(-x)=-f(x),∴f(x)是奇函数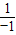 =-2,又f(1)=1+
=-2,又f(1)=1+ =2
=2