题目内容
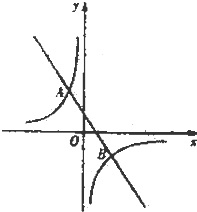 如图,一次函数f(x)=kx+b的图象与反比例函数g(x)=
如图,一次函数f(x)=kx+b的图象与反比例函数g(x)=| m |
| x |
(1)求这两个函数的解析式;
(2)求函数g(x)=g(x)=
| m |
| x |
分析:(1)f(x)、g(x)的图象都过点A和B,把点的坐标代入解析式,即得所求;
(2)由函数图象知g(x)在[1,4]上是增函数,在端点处求得最值;
(2)由函数图象知g(x)在[1,4]上是增函数,在端点处求得最值;
解答:解:(1)∵函数g(x)=
的图象过点A(-2,6),
∴m=-2×6=-12,
∴g(x)=-
;
又g(x)的图象过点B(4,n),
∴n=-
=-3;
又函数f(x)=kx+b的图象过点A和点B,
∴
,解得k=-
,b=3;
∴f(x)=-
x+3.
(2)由于函数g(x)=-
,g(x)的图象在(0,+∞)内从左向右是上升的,是增函数,
∴g(x)在[1,4]上是增函数;
∴函数g(x)在[1,4]上的最大值为g(4)=-3,
最小值为g(1)=-12.
| m |
| x |
∴m=-2×6=-12,
∴g(x)=-
| 12 |
| x |
又g(x)的图象过点B(4,n),
∴n=-
| 12 |
| 4 |
又函数f(x)=kx+b的图象过点A和点B,
∴
|
| 3 |
| 2 |
∴f(x)=-
| 3 |
| 2 |
(2)由于函数g(x)=-
| 12 |
| x |
∴g(x)在[1,4]上是增函数;
∴函数g(x)在[1,4]上的最大值为g(4)=-3,
最小值为g(1)=-12.
点评:本题考查了利用待定系数法求函数的解析式,利用函数图象判定单调性,利用单调性求最值问题.

练习册系列答案
相关题目
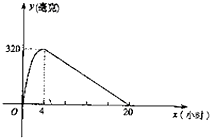 某种新药服用x小时后血液中的残留量为y毫克,如图为函数y=f(x)的图象,在x∈(0,4]时为二次函数,且当x=4时到达顶点;在x∈(4,20]为一次函数,当血液中药物残留量不小于240毫克时,治疗有效.
某种新药服用x小时后血液中的残留量为y毫克,如图为函数y=f(x)的图象,在x∈(0,4]时为二次函数,且当x=4时到达顶点;在x∈(4,20]为一次函数,当血液中药物残留量不小于240毫克时,治疗有效.