题目内容
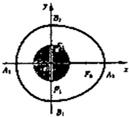 如图,一个熟鸡蛋的轴截面由半椭圆
如图,一个熟鸡蛋的轴截面由半椭圆| x2 |
| a2 |
| y2 |
| b2 |
| y2 |
| b2 |
| x2 |
| c2 |
| π |
| 6 |
| A、5,3 | ||||
B、
| ||||
C、
| ||||
| D、5,4 |
分析:由题意知|F1F2|=|F1F0|=|F2F0|=2
,
=cos30°,b=
c,再由蛋黄的体积是
,F1,F2在蛋黄球面上,知
π(
)3=
,由此可求出a和b.
| b2-c2 |
| c | ||
2
|
2
| ||
| 3 |
| π |
| 6 |
| 4 |
| 3 |
| b2-a2 |
| π |
| 6 |
解答:解:由题意知|F1F2|=|F1F0|=|F2F0|=2
,
∴
=cos30°,
∴b=
c∵蛋黄的体积是
,F1,F2在蛋黄球面上,
∴R=
,
∴
π(
)3=
,∴b2-c2=
,
∴
c2-c2=
,c2=
,b2=1,a2=
,
故a=
,b=1,
故选C.
| b2-c2 |
∴
| c | ||
2
|
∴b=
2
| ||
| 3 |
| π |
| 6 |
∴R=
| b2-a2 |
∴
| 4 |
| 3 |
| b2-a2 |
| π |
| 6 |
| 1 |
| 4 |
∴
| 12 |
| 9 |
| 1 |
| 4 |
| 3 |
| 4 |
| 7 |
| 4 |
故a=
| ||
| 2 |
故选C.
点评:本题巧妙地把两个椭圆合二为一,具有一定的难度,解题时要熟练掌握椭圆的性质和公式.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
 如图,一个熟鸡蛋的轴截面由半椭圆
如图,一个熟鸡蛋的轴截面由半椭圆 +
+ =1(x≥0)与半椭圆
=1(x≥0)与半椭圆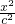 =1(x<0)合成(其中a2=b2+c2,a>b>c>0).设点F0,F1,F2是相应椭圆的焦点,A1、A2和B1、B2是轴截面与x,y轴的交点,阴影部分是蛋黄(球形)轴截面,若蛋黄的体积是
=1(x<0)合成(其中a2=b2+c2,a>b>c>0).设点F0,F1,F2是相应椭圆的焦点,A1、A2和B1、B2是轴截面与x,y轴的交点,阴影部分是蛋黄(球形)轴截面,若蛋黄的体积是 ,F1,F2在蛋黄球面上,△F0F1F2是等边三角形,则a,b的值分别为
,F1,F2在蛋黄球面上,△F0F1F2是等边三角形,则a,b的值分别为 ,1
,1 ,1
,1 +
+ =1(x≥0)与半椭圆
=1(x≥0)与半椭圆 +
+ =1(x<0)合成(其中a2=b2+c2,a>b>c>0).设点F,F1,F2是相应椭圆的焦点,A1、A2和B1、B2是轴截面与x,y轴的交点,阴影部分是蛋黄(球形)轴截面,若蛋黄的体积是
=1(x<0)合成(其中a2=b2+c2,a>b>c>0).设点F,F1,F2是相应椭圆的焦点,A1、A2和B1、B2是轴截面与x,y轴的交点,阴影部分是蛋黄(球形)轴截面,若蛋黄的体积是 ,F1,F2在蛋黄球面上,△FF1F2是等边三角形,则a,b的值分别为( )
,F1,F2在蛋黄球面上,△FF1F2是等边三角形,则a,b的值分别为( )
 ,1
,1 ,1
,1 +
+ =1(x≥0)与半椭圆
=1(x≥0)与半椭圆 +
+ =1(x<0)合成(其中a2=b2+c2,a>b>c>0).设点F,F1,F2是相应椭圆的焦点,A1、A2和B1、B2是轴截面与x,y轴的交点,阴影部分是蛋黄(球形)轴截面,若蛋黄的体积是
=1(x<0)合成(其中a2=b2+c2,a>b>c>0).设点F,F1,F2是相应椭圆的焦点,A1、A2和B1、B2是轴截面与x,y轴的交点,阴影部分是蛋黄(球形)轴截面,若蛋黄的体积是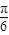 ,F1,F2在蛋黄球面上,△FF1F2是等边三角形,则a,b的值分别为( )
,F1,F2在蛋黄球面上,△FF1F2是等边三角形,则a,b的值分别为( )
 ,1
,1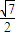 ,1
,1