题目内容
设向量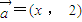
，
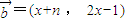（n为正整数），函数
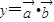在[0，1]上的最小值与最大值的和为an，又数列{bn}满足：
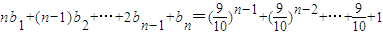．（1）求证：an=n+1（2）．
（2）求bn的表达式．
（3）若cn=-an•bn，试问数列{cn}中，是否存在正整数k，使得对于任意的正整数n，都有cn≤ck成立？证明你的结论．（注：
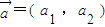与
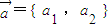表示意义相同）
【答案】分析：（1）对称轴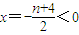
，所以y=x2+（n+4）x-2在[0，1]上为增函数，故可证；
（2）由数列{bn}满足的条件，再写一式，两式相减可求；
（3）设存在自然数k，使对n∈N，cn≤ck恒成立，易得当n＜8时，cn+1＞cn，当n=8时，cn+1=cn，当n＞8时，cn+1＜cn故得解．
解答：解：（1）证明：对称轴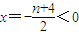
，所以y=x2+（n+4）x-2在[0，1]上为增函数---（2分）
an=（-2）+（n+3）=n+1--（4分）
（2）解：由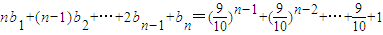
，
得，（n-1）b1+（n-2）b2+…+bn-1=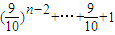
两式相减，
得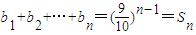
∴当n=1时，b1=S1=1
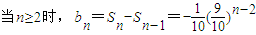
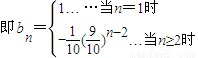
（3）由（1）与（2）得
设存在自然数k，使对n∈N，cn≤ck恒成立
当n=1时，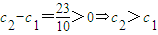
当n≥2时，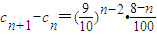
，
∴当n＜8时，cn+1＞cn
当n=8时，cn+1=cn，当n＞8时，cn+1＜cn
所以存在正整数k=9，使对任意正整数n，均有c1＜c2＜…＜c8=c9＞c10＞c11＞…
点评：本题考查数列的性质及其应用，难度较大，解题时要认真审题，仔细解答．
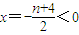，所以y=x2+（n+4）x-2在[0，1]上为增函数，故可证；（2）由数列{bn}满足的条件，再写一式，两式相减可求；
（3）设存在自然数k，使对n∈N，cn≤ck恒成立，易得当n＜8时，cn+1＞cn，当n=8时，cn+1=cn，当n＞8时，cn+1＜cn故得解．
解答：解：（1）证明：对称轴
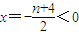，所以y=x2+（n+4）x-2在[0，1]上为增函数---（2分）an=（-2）+（n+3）=n+1--（4分）
（2）解：由
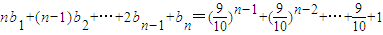，得，（n-1）b1+（n-2）b2+…+bn-1=
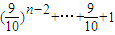两式相减，得
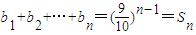
∴当n=1时，b1=S1=1
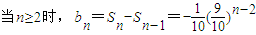
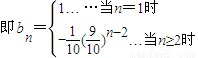
（3）由（1）与（2）得
设存在自然数k，使对n∈N，cn≤ck恒成立
当n=1时，
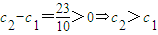
当n≥2时，
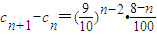，∴当n＜8时，cn+1＞cn
当n=8时，cn+1=cn，当n＞8时，cn+1＜cn
所以存在正整数k=9，使对任意正整数n，均有c1＜c2＜…＜c8=c9＞c10＞c11＞…
点评：本题考查数列的性质及其应用，难度较大，解题时要认真审题，仔细解答．
练习册系列答案
相关题目
，
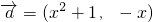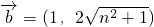（n为正整数），函数
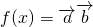，设f（x）在（0，+∞）上取最小值时的自变量x取值为an．
；
，
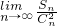（n为正整数），函数
，设f（x）在（0，+∞）上取最小值时的自变量x取值为an．
；
，
（n为正整数），函数
，设f（x）在（0，+∞）上取最小值时的自变量x取值为an．
；
，
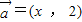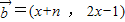（n为正整数），函数
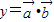在[0，1]上的最小值与最大值的和为an，又数列{bn}满足：
．
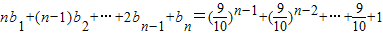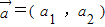与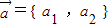
表示意义相同）