题目内容
已知正项数列{an}中a1=2,点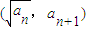 在函数
在函数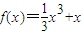 的导函数y=f'(x)图象上,数列{bn}中,点(bn,Sn)在直线
的导函数y=f'(x)图象上,数列{bn}中,点(bn,Sn)在直线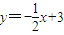 上,其中Sn是数列{bn}的前n项和(n∈N*)
上,其中Sn是数列{bn}的前n项和(n∈N*)(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)若数列{cn}满足
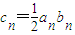 ,且数列{cn}的前n项和Tn,求证:
,且数列{cn}的前n项和Tn,求证: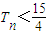 .
.
【答案】分析:(Ⅰ)由函数 ,知f′(x)=x2+1,由正项数列{an}中,点
,知f′(x)=x2+1,由正项数列{an}中,点 在函数
在函数 的导函数y=f'(x)图象上,知an+1=an+1,由此能求出数列{an}的通项公式;数列{bn}中,点(bn,Sn)在直线
的导函数y=f'(x)图象上,知an+1=an+1,由此能求出数列{an}的通项公式;数列{bn}中,点(bn,Sn)在直线 上,故
上,故 ,由此能求出数列{bn}的通项公式.
,由此能求出数列{bn}的通项公式.
(Ⅱ)由 =
= =
= ,知
,知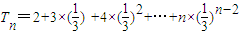
 ,用错位相减法能够证明
,用错位相减法能够证明 -(n+1)×
-(n+1)× ≤
≤ .
.
解答:(Ⅰ)解:∵函数 ,
,
∴f′(x)=x2+1,
∵正项数列{an}中,点 在函数
在函数 的导函数y=f'(x)图象上,
的导函数y=f'(x)图象上,
∴an+1=an+1,
∵a1=2,
∴an=2+(n-1)=n+1.
∵数列{bn}中,点(bn,Sn)在直线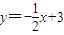 上,
上,
∴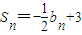 ,①
,①
∴ ,
,
解得b1=2.
 ,②
,②
①-②,得 ,
,
∴ ,
,
∴ ,
,
∴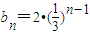 .
.
(Ⅱ)证明:∵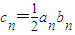 =
= =
= ,
,
∴
 ,
,
 +…+
+…+ ,
,
∴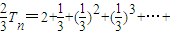
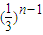 -(n+1)×
-(n+1)×
=2+ -(n+1)×
-(n+1)×
=2+ -
- -(n+1)×
-(n+1)× ,
,
∴ -(n+1)×
-(n+1)×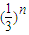 ≤
≤ .
.
点评:本题考查数列与函数的综合,考查数列通项公式的求法和数列前n项和的证明,解题时要认真审题,注意错位相减求和法的合理运用.
 ,知f′(x)=x2+1,由正项数列{an}中,点
,知f′(x)=x2+1,由正项数列{an}中,点 在函数
在函数 的导函数y=f'(x)图象上,知an+1=an+1,由此能求出数列{an}的通项公式;数列{bn}中,点(bn,Sn)在直线
的导函数y=f'(x)图象上,知an+1=an+1,由此能求出数列{an}的通项公式;数列{bn}中,点(bn,Sn)在直线 上,故
上,故 ,由此能求出数列{bn}的通项公式.
,由此能求出数列{bn}的通项公式.(Ⅱ)由
 =
= =
= ,知
,知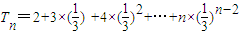
 ,用错位相减法能够证明
,用错位相减法能够证明 -(n+1)×
-(n+1)× ≤
≤ .
.解答:(Ⅰ)解:∵函数
 ,
,∴f′(x)=x2+1,
∵正项数列{an}中,点
 在函数
在函数 的导函数y=f'(x)图象上,
的导函数y=f'(x)图象上,∴an+1=an+1,
∵a1=2,
∴an=2+(n-1)=n+1.
∵数列{bn}中,点(bn,Sn)在直线
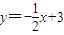 上,
上,∴
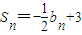 ,①
,①∴
 ,
,解得b1=2.
 ,②
,②①-②,得
 ,
,∴
 ,
,∴
 ,
,∴
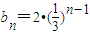 .
.(Ⅱ)证明:∵
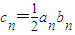 =
= =
= ,
,∴

 ,
, +…+
+…+ ,
,∴
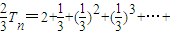
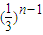 -(n+1)×
-(n+1)×
=2+
 -(n+1)×
-(n+1)×
=2+
 -
- -(n+1)×
-(n+1)× ,
,∴
 -(n+1)×
-(n+1)×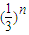 ≤
≤ .
.点评:本题考查数列与函数的综合,考查数列通项公式的求法和数列前n项和的证明,解题时要认真审题,注意错位相减求和法的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目