题目内容
已知Sn是{an}的前n项和，且有Sn=2an-1，则数列{an}的通项an=______．
当n=1时，a1=S1=2a1-1，∴a1=1．
当n＞1时，Sn=2an-1，∴Sn-1=2an-1-1，
∴Sn-Sn-1=2an-2an-1，
∴an=2an-2an-1，
∴an=2an-1，
∴
=2，
∴{an}是首贡为1，公比为2的等比数列，∴an=2n-1，n∈N*．
答案：an=2n-1，n∈N*．
当n＞1时，Sn=2an-1，∴Sn-1=2an-1-1，
∴Sn-Sn-1=2an-2an-1，
∴an=2an-2an-1，
∴an=2an-1，
∴
| an |
| an-1 |
∴{an}是首贡为1，公比为2的等比数列，∴an=2n-1，n∈N*．
答案：an=2n-1，n∈N*．
练习册系列答案
相关题目
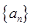是公差为2的等差数列，
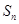是
= ．
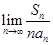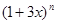展开式中，二项式系数之和为
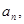各项系数之和为
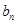则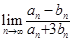
= . 
= 。