题目内容
(本小题满分14分) 已知数列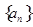 的前
的前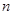 项和为
项和为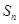 ,且
,且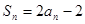
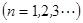 ,等差数列
,等差数列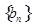 中,
中,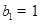 ,
,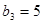 。
。
(1)求数列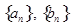 的通项
的通项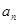 和
和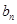 ;
;
(2) 设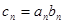 ,求数列
,求数列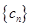 的前
的前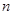 项和
项和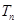 ,
,
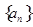 的前
的前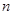 项和为
项和为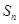 ,且
,且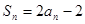
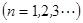 ,等差数列
,等差数列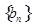 中,
中,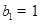 ,
,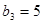 。
。(1)求数列
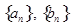 的通项
的通项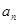 和
和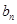 ;
;(2) 设
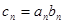 ,求数列
,求数列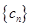 的前
的前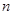 项和
项和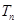 ,
, 解(1) ;
;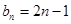 ;(II)
;(II) 。
。
 ;
;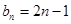 ;(II)
;(II) 。
。本试题主要是考查了运用前n项和与通项公式之间的关系式的运用,以及数列求和的综合问题。
(1) ,两式作差,得到
,两式作差,得到

然后利用递推关系得到等比数列,聪的得到通项公式的结论。
(2) ,那么利用错位相减法可知数列的和 。
,那么利用错位相减法可知数列的和 。
解(1)

 …………………………………2分
…………………………………2分 

设等差数列 的公差为
的公差为 ,
, 得到
得到 ……………………6分
……………………6分
 …………………………………8分
…………………………………8分
(II)
 ……9分
……9分
 ……………………10分
……………………10分
因此: ……11分
……11分
即: ……………………12分
……………………12分
 ………………………14分
………………………14分
(1)
 ,两式作差,得到
,两式作差,得到
然后利用递推关系得到等比数列,聪的得到通项公式的结论。
(2)
 ,那么利用错位相减法可知数列的和 。
,那么利用错位相减法可知数列的和 。解(1)


 …………………………………2分
…………………………………2分 

设等差数列
 的公差为
的公差为 ,
, 得到
得到 ……………………6分
……………………6分 …………………………………8分
…………………………………8分(II)

 ……9分
……9分 ……………………10分
……………………10分因此:
 ……11分
……11分即:
 ……………………12分
……………………12分 ………………………14分
………………………14分
练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
 中,
中, ,
, (
( ),数列
),数列 项和为
项和为 。(1)证明:数列
。(1)证明:数列 是等比数列,并求数列
是等比数列,并求数列 。
。 满足
满足 ,
, (
( ).
). 是等差数列;
是等差数列; ;
; ,求数列
,求数列 的前
的前 项和
项和 .
. 的前
的前 项和为
项和为 .已知
.已知 ,
, ,
, 。
。 为数列
为数列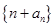 的前
的前 中,
中, ,
, 是方程
是方程 的两个根,则数列
的两个根,则数列 前
前 项和
项和 ( )
( )



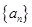 的前
的前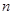 项和
项和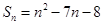 ,
,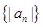 的前
的前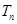 .
.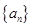 满足
满足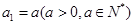 ,
,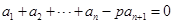
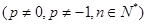 .
.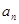 ;
;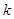 ,若将
,若将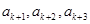 按从小到大的顺序排列后,此三项均能构成等
按从小到大的顺序排列后,此三项均能构成等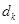 .①求
.①求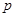 的值及对应的数列
的值及对应的数列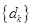 .
.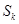 为数列
为数列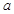 ,使得
,使得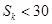 对任意正整数
对任意正整数 的通项公式为
的通项公式为 ,则
,则 ( )
( )

 的前
的前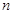 项和
项和 ____________.
____________.