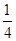题目内容
已知点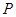 在曲线
在曲线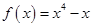 上,曲线在点
上,曲线在点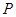 处的切线平行于直线
处的切线平行于直线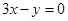 ,则点
,则点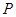 的坐标为
的坐标为
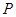 在曲线
在曲线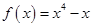 上,曲线在点
上,曲线在点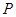 处的切线平行于直线
处的切线平行于直线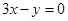 ,则点
,则点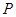 的坐标为
的坐标为A.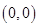 | B.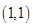 | C.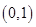 | D.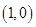 |
D
试题分析:由曲线的解析式求出y的导函数,因为曲线上过点P的切线方程平行于直线y=3x+2,得到两直线的斜率相等,由y=3x+2求出直线的斜率,令导函数等于求出的斜率,列出关于x的方程,求出方程的解即可得到x的值即为点P的横坐标,把求出的x的值代入曲线解析式中求出的y即为点P的纵坐标,写出点P的坐标即可。解:由y=x4-x,得到y′=4x3-1,又直线y=3x+2的斜率为3,
则4x3-1=3,解得x=1,把x=1代入曲线方程得:y=0,所以点P的坐标为(1,0).故答案为:D
点评:此题要求学生掌握两直线平行时斜率相等,会利用导数求曲线上过某点切线方程的斜率,是一道中档题.

练习册系列答案
相关题目
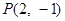 为圆
为圆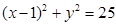 的弦
的弦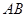 的中点,则直线
的中点,则直线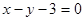
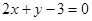
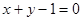
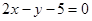
 ,若
,若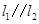 ,则
,则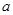 =______
=______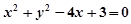 有公共点,则直线的倾斜角的取值范围是( )
有公共点,则直线的倾斜角的取值范围是( )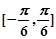
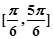
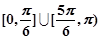
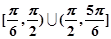
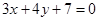 和直线
和直线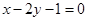 的交点坐标是( )
的交点坐标是( )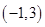
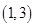
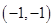

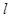 经过点P(-5,-4),且与两坐标轴围成的三角形面积为5,求直线
经过点P(-5,-4),且与两坐标轴围成的三角形面积为5,求直线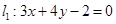 与
与 的交点
的交点 ,求:(1)过点
,求:(1)过点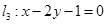 的直线
的直线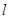 的方程。
的方程。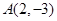 ,
,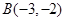 ,直线
,直线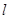 过点
过点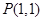 且与线段
且与线段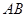 相交,则
相交,则 的取值范围是( )
的取值范围是( )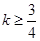 或
或
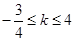

 或
或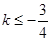
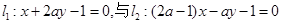 平行,则
平行,则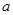 的值是( )
的值是( )