题目内容

A（2，-2）点为坐标平面上的一个点，B（a，b）点为坐标平面上的一点，O点为坐标原点，记“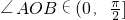 $数学公式$ ”为事件C．
（1）若将一粒骰子连续抛掷两次（骰子是有六个面的正方体且每个面分别标有1，2，3，4，5，6）得到点数分别记为a，b，求事件C发生的概率；
（2）若a、b均为从区间[0，6]内任取的一个数，记事件D表示“|a-b|＜2”，求事件D发生的概率．

解：（1）设得到点数分别记为a，b，用（a，b）表示一个基本事件，
则抛掷两次骰子的所有基本事件有：
（1，1），（1，2），（1，3），（1，4），（1，5），（1，6），（2，1），（2，2），…，（6，5），（6，6），共36个．（2分）
事件C包含的基本事件有：（1，1），（2，1），（2，2），…，（6，6）共1+2+3+4+5+6=21个．
∴P（A）= $\text{[math]}$
答：事件C的概率为 $\text{[math]}$ ．
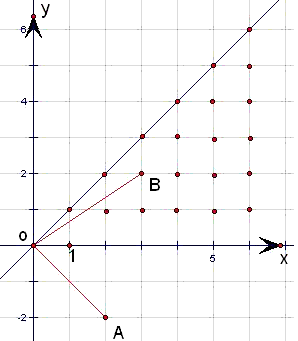
（2）试验的全部结果所构成的区域为：
{（a，b）|0≤a≤6，0≤b≤6}
构成事件D的区域为：
{（a，b）|0≤a≤6，0≤b≤6，a-b≥0}
所以所求的概率为P（B）= $\text{[math]}$
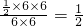
答：事件D的概率为 $\text{[math]}$ ．
分析：（1）本小题考查的知识点是古典概型，关键是要找出满足事件C的基本事件个数，及总的基本事件的个数，再代入古典概型公式进行计算求解．
（2）本小题考查的知识点是几何概型的意义，关键是要画出满足事件D对应的图形，结合图形分析，找出满足条件的点集对应的图形面积，及图形的总面积．
点评：古典概型要求所有结果出现的可能性都相等，强调所有结果中每一结果出现的概率都相同．弄清一次试验的意义以及每个基本事件的含义是解决问题的前提，正确把握各个事件的相互关系是解决问题的关键．解决问题的步骤是：计算满足条件的基本事件个数，及基本事件的总个数，然后代入古典概型计算公式进行求解．
几何概型的概率估算公式中的“几何度量”，可以为线段长度、面积、体积等，而且这个“几何度量”只与“大小”有关，而与形状和位置无关．解决的步骤均为：求出满足条件A的基本事件对应的“几何度量”N（A），再求出总的基本事件对应的“几何度量”N，最后根据P= 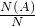$\text{[math]}$ 求解．