题目内容
已知非零向量A.等边三角形 B.等腰非等边三角形
C.直角三角形 D.三边均不等的三角形
答案:A
解析:∵![]() +
+![]() 与∠BAC的角平分线
与∠BAC的角平分线![]() 同向,
同向,
由(![]() +
+![]() )·
)·![]() =0,可知
=0,可知![]() ⊥
⊥![]() ,
,
故|![]() |=|
|=|![]() |.又
|.又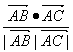 =
=![]() =cos
=cos![]() ,∴∠BAC=
,∴∠BAC=![]() .
.
∴△ABC为等边三角形.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
题目内容
已知非零向量A.等边三角形 B.等腰非等边三角形
C.直角三角形 D.三边均不等的三角形
答案:A
解析:∵![]() +
+![]() 与∠BAC的角平分线
与∠BAC的角平分线![]() 同向,
同向,
由(![]() +
+![]() )·
)·![]() =0,可知
=0,可知![]() ⊥
⊥![]() ,
,
故|![]() |=|
|=|![]() |.又
|.又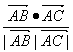 =
=![]() =cos
=cos![]() ,∴∠BAC=
,∴∠BAC=![]() .
.
∴△ABC为等边三角形.

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案