题目内容
若椭圆的对称轴在坐标轴,两焦点与两短轴的端点恰好是正方形的四个顶点,且焦点到同侧长轴端点距离为
-1.
(1)求椭圆方程;
(2)求椭圆离心率.
| 2 |
(1)求椭圆方程;
(2)求椭圆离心率.
分析:(1)由题意推出椭圆的关系,b=c,利用焦点到同侧长轴端点距离为
-1,
(2)通过椭圆方程,求出椭圆的离心率.
| 2 |
(2)通过椭圆方程,求出椭圆的离心率.
解答:解:(1)因为椭圆的对称轴在坐标轴,两焦点与两短轴的端点恰好是正方形的四个顶点,
所以b=c,a=
b,又焦点到同侧长轴端点距离为
-1,
即a-c=
-1,即a-b=
-1,解得a=
,b=c=1,
所以当焦点在x轴时,椭圆的方程为:
+y2=1;
当焦点在y轴时,椭圆的方程为
+x2=1.
(2)由(1)可知a=
,b=c=1,所以椭圆的离心率为:
=
.
所以b=c,a=
| 2 |
| 2 |
即a-c=
| 2 |
| 2 |
| 2 |
所以当焦点在x轴时,椭圆的方程为:
| x2 |
| 2 |
当焦点在y轴时,椭圆的方程为
| y2 |
| 2 |
(2)由(1)可知a=
| 2 |
| c |
| a |
| ||
| 2 |
点评:本题考查椭圆的方程的求法,椭圆的基本性质,离心率的求法,考查计算能力.

练习册系列答案
相关题目
 可把平面直角坐标系上的一点
可把平面直角坐标系上的一点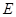 的中心在坐标原点、对称轴为坐标轴,且抛物线
的中心在坐标原点、对称轴为坐标轴,且抛物线 的焦点是它的一个焦点,又点
的焦点是它的一个焦点,又点 在该椭圆上.
在该椭圆上. 直线
直线 与椭圆
与椭圆 ,当
,当 面积的最大值时,求直线
面积的最大值时,求直线 :
: 可把平面直角坐标系上的点
可把平面直角坐标系上的点 变换到这一平面上的点
变换到这一平面上的点 .特别地,若曲线
.特别地,若曲线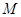 上一点
上一点 经变换公式
经变换公式 与点
与点 的中心为坐标原点,焦点在
的中心为坐标原点,焦点在 轴上,且焦距为
轴上,且焦距为 ,长轴顶点和短轴顶点间的距离为2. 求该椭圆
,长轴顶点和短轴顶点间的距离为2. 求该椭圆 时,其两个焦点
时,其两个焦点 、
、 经变换公式
经变换公式 和
和 的坐标;
的坐标; ,
, )下的不动点的存在情况和个数.
)下的不动点的存在情况和个数. :
: 可把平面直角坐标系上的一点
可把平面直角坐标系上的一点 变换到这一平面上的一点
变换到这一平面上的一点 .
. 的中心为坐标原点,焦点在
的中心为坐标原点,焦点在 轴上,且焦距为
轴上,且焦距为 ,长轴顶点和短轴顶点间的距离为2. 求该椭圆
,长轴顶点和短轴顶点间的距离为2. 求该椭圆 、
、 经变换公式
经变换公式 和
和 的坐标;
的坐标; 上一点
上一点 经变换公式
经变换公式 与点
与点