题目内容
已知首项为正数的等差数列{an}的前n项和为Sn,若a1 006和a1 007是方程x2-2 012x-2 011=0的两根,则使Sn>0成立的正整数n的最大值是( ).
| A.1006 | B.1007 | C.2011 | D.2012 |
C
解析试题分析:根据题意,利用根与系数的关系可知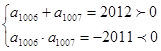 ,又因为该等差数列的首项为正数,所以该数列是首项为正数的递减数列,且
,又因为该等差数列的首项为正数,所以该数列是首项为正数的递减数列,且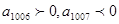 ,
,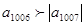 ,即该数列从第1007项开始为负数.所以有
,即该数列从第1007项开始为负数.所以有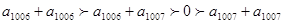 ,则要求使
,则要求使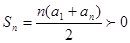 成立的最大正整数
成立的最大正整数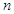 的值,就是求使
的值,就是求使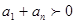 成立得最大正整数
成立得最大正整数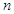 的值.根据等差数列的性质:当
的值.根据等差数列的性质:当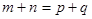 时,有
时,有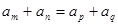 .显然此时
.显然此时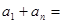
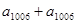 ,可得
,可得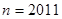 .
.
考点:二次方程根与系数的关系;等差数列性质当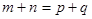 时,有
时,有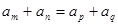 的使用.
的使用.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
在等差数列{an}中,其前n项和是 ,若
,若 ,则在
,则在 中最大的是( )
中最大的是( )
A. | B. | C. | D. |
数列 :
: 、3、
、3、 、9、的一个通项公式是( )
、9、的一个通项公式是( )
A.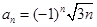 ( (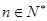 ) ) | B. ( (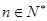 ) ) |
C. ( (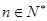 ) ) | D. ( (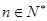 ) ) |
现有数列 满足:
满足: ,且对任意的m,n∈N*都有:
,且对任意的m,n∈N*都有: ,则
,则 ( )
( )
A. | B. | C. | D. |
已知数列{ }中,
}中, =
= ,
, +
+ (n
(n ,则数列{
,则数列{ }的通项公式为( )
}的通项公式为( )
A. | B. |
C. | D. |
已知函数 的图象与直线
的图象与直线 交于点P,若图象在点P处的切线与x轴交点的横坐标为
交于点P,若图象在点P处的切线与x轴交点的横坐标为 ,则
,则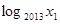 +
+ +…+
+…+ 的值为( )
的值为( )
| A.-1 | B.1-log20132012 | C.-log20132012 | D.1 |
 的各项均为正数,
的各项均为正数, 为其前
为其前 项和,且对任意的
项和,且对任意的 ,有
,有 .
. ,求数列
,求数列 的前
的前 .
. 

 的图像如下列图中,经过原点和(1,1),且对任意
的图像如下列图中,经过原点和(1,1),且对任意 ,由关系式
,由关系式 得到数列{
得到数列{ },满足
},满足 ,则该函数的图像为( )
,则该函数的图像为( )