题目内容
设数列![]() 满足
满足![]() ,令
,令![]() .
.
⑴试判断数列![]() 是否为等差数列?并求数列
是否为等差数列?并求数列![]() 的通项公式;
的通项公式;
⑵令![]() ,是否存在实数
,是否存在实数![]() ,使得不等式
,使得不等式![]() 对一切
对一切
![]() 都成立?若存在,求出
都成立?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
解析: ⑴由已知得![]() ,
,
即![]() , …………2分
, …………2分
所以![]() ,即
,即![]() ,
,
又![]() ,所以数列
,所以数列![]() 为等差数列,通项公式为
为等差数列,通项公式为![]() . …………6分
. …………6分
(2)令![]()
![]() ,由
,由![]() ,得
,得
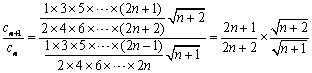
![]()
所以,数列![]() 为单调递减数列, …………8分
为单调递减数列, …………8分
所以数列![]() 的最大项为
的最大项为![]() ,
,
若不等式![]() 对一切
对一切![]() 都成立,只需
都成立,只需![]() ,解得
,解得![]() ,
,
又![]() ,所以
,所以![]() 的取值范围为
的取值范围为![]() . …………12分
. …………12分
(3)问题可转化为比较![]() 与
与![]() 的大小.设函数
的大小.设函数![]() ,所以
,所以![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .所以
.所以![]() 在
在![]() 上为增函数;
上为增函数;
在![]() 上为减函数.
上为减函数.
当![]() 时,显然有
时,显然有![]() ,
,
当![]() 时,
时,![]() ,即
,即![]() ,所以
,所以![]() ,
,
即![]() 所以
所以![]() .
.
综上:当![]() 时,
时,![]() ,即
,即![]() ;
;

练习册系列答案
 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
 满足
满足 ,令
,令 .
.  是否为等差数列?并说明理由;
是否为等差数列?并说明理由; ,求
,求 前
前 项的和
项的和 ;
; 使得
使得 三数成等比数列?
三数成等比数列? 满足
满足 ,令
,令 .
.  是否为等差数列?并说明理由;
是否为等差数列?并说明理由; ,求
,求 前
前 项的和
项的和 ;
; 使得
使得 三数成等比数列?
三数成等比数列?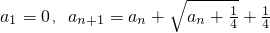 ,令
,令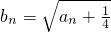 .
.