题目内容

若实数x，y，m，n满足x2+y2=2，m2+n2=1，则mx+ny的最大值是（　　）
分析：利用三角换元，将其代入mx+ny中，由三角函数公式分析可得答案．
解答：解：令m=cosα，n=sinα，x=
2
cosβ，y=
2
sinβ，
则mx+ny=
2
cosαcosβ+
2
sinαsinβ=
2
cos（α-β）≤
2

∴mx+ny的最大值是
2

故选B．
点评：本题主要考查求最值问题，考查三角换元，属于基础题．
练习册系列答案
相关题目
若实数x，y，m满足|x-m|＜|y-m|，则称x比y靠近m．
（Ⅰ）若x+1比-x靠近-1，求实数x的取值范围；
（Ⅱ）①对任意x＞0，证明：ln（1+x）比x靠近0；②已知数列{an}的通项公式为an=1+21-n，证明：a1a2a3…an＜2e．

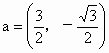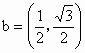(2006河南省实验中学模拟)若平面向量，，且存在实数x和y，使得，n=－ya＋xb，且m⊥n．

(1)求y=f(x)的关系式，并求其单调区间；

(2)点P在曲线y=f(x)上移动时，求过点P的切线的倾斜角θ的取值范围；

(3)若y=f(x)与y=k有三个交点，求k的取值范围．

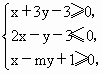若实数x，y满足不等式组，且x＋y的最大值为9，则实数m、n

[　　]
A．

－2

B．

－1

C．

1

D．

2
若实数x，y，m，n满足x2+y2=2，m2+n2=1，则mx+ny的最大值是（　　）
A．1B．
2
C．
3
D．2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网