题目内容
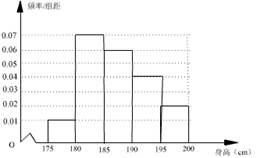
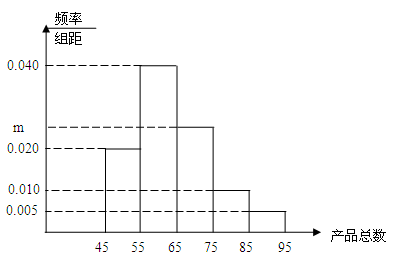
某大学体育学院在2012年新招的大一学生中,随机抽取了 40名男生,他们的身高(单位:cm)情况共分成五组:第1组[175,180),第 2 组[180,185),第 3 组 [185,190),第 4 组[190,195),第 5 组[195,200) .得到的频率分布直方图(局部)如图所示,同时规定身高在185cm以上(含185cm)的学生成为组建该校篮球队的“预备生”.

(I)求第四组的频率并补布直方图;
(II)如果用分层抽样的方法从“预备生”和“非预备生”中选出5人,再从这5人中随机选2人,那么至少有1人是“预备生”的概率是多少?
(III)若该校决定在第4,5组中随机抽取2名学生接受技能测试,第5组中有ζ名学生接受测试,试求ζ的分布列和数学期望.

(I)求第四组的频率并补布直方图;
(II)如果用分层抽样的方法从“预备生”和“非预备生”中选出5人,再从这5人中随机选2人,那么至少有1人是“预备生”的概率是多少?
(III)若该校决定在第4,5组中随机抽取2名学生接受技能测试,第5组中有ζ名学生接受测试,试求ζ的分布列和数学期望.
(I) 第四组的频率为0.2 (II)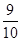
(III) 分布列为:
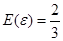
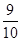
(III) 分布列为:
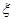 | 0 | 1 | 2 |
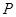 | 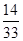 | 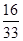 | 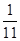 |
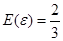
试题分析:(Ⅰ)其它组的频率和为(0.01+0.07+0.06+0.02)×5=0.8,所以第四组的频率为0.2 ……3分
(Ⅱ)依题意“预备生”和“非预备生”的人数比为3:2,所以采用分层抽样的方法抽取的5人中有“预备生”3人,“非预备生” 2人,记从这5人中选2人至少有1人是“预备生”为事件
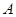
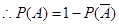 =
=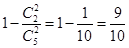 . ……6分
. ……6分(Ⅲ)由频率分布直方图可知,第四组的人数为8人,第五组的人数为4人
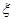 的所有可能取值为0,1,2
的所有可能取值为0,1,2 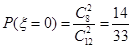 ,
,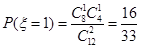 ,
,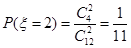 ……9分
……9分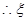 的分布列为:
的分布列为: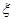 | 0 | 1 | 2 |
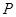 | 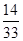 | 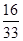 | 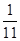 |
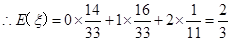 ……12分
……12分点评:解决有关频率分布直方图问题时,要注意纵轴是频率/组距,而不是频率;写离散型随机变量的分布列时,要准确写出随机变量取不同值时的概率,可以利用概率和为1检验是写的分布列否正确.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的分布表如下:
的分布表如下:
 个;
个; 个;
个; 个;
个; 个;
个; 个;
个; 个。则样本在区间
个。则样本在区间 上的频率为
上的频率为
 ,
,
 ,
,  ,
, ,
, .则图中
.则图中 的值为( )
的值为( )

 男 女
男 女 15 7 7 8 9 9 9
15 7 7 8 9 9 9