题目内容
 定义域为R的函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
定义域为R的函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π | 2 |
(1)f(x)的表达式;
(2)f(x)的单调增区间;
(3)f(x)的对称轴和对称中心;
(4)f(x)的最小值以及取得最小值时的x的集合.
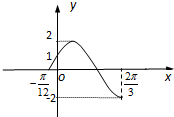
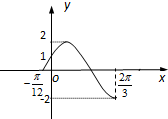
分析:(1)由图知,
T=
,从而可求得ω=2,由-
×2+φ=2kπ(k∈Z),|φ|<
,可求得φ,从而得f(x)的表达式;
(2)利用正弦函数的单调性,解不等式-
+2kπ≤2x+
≤
+2kπ,k∈Z即可求得f(x)的单调增区间;
(3)利用正弦函数的对称性即可求得f(x)=2sin(2x+
)的对称轴方程及对策中心;
(4)由正弦函数的最值性质可求得f(x)的最小值以及取得最小值时的x的集合.
| 3 |
| 4 |
| 3π |
| 4 |
| π |
| 12 |
| π |
| 2 |
(2)利用正弦函数的单调性,解不等式-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
(3)利用正弦函数的对称性即可求得f(x)=2sin(2x+
| π |
| 6 |
(4)由正弦函数的最值性质可求得f(x)的最小值以及取得最小值时的x的集合.
解答:解:(1)由图知A=2,
•
=
-(-
)=
,
∴ω=2,
又-
×2+φ=2kπ(k∈Z),
∴φ=2kπ+
(k∈Z),
又|φ|<
,
∴φ=
,
∴f(x)=2sin(2x+
);
(2)由-
+2kπ≤2x+
≤
+2kπ,k∈Z得:kπ-
≤x≤
+kπ,k∈Z,
∴f(x)的单调增区间为[kπ-
,
+kπ](k∈Z);
(3)由2x+
=
+kπ(k∈Z)得:x=
+k
(k∈Z),
∴其对称轴方程为:x=
+k
(k∈Z);
由2x+
=kπ(k∈Z),得x=
-
,k∈Z.
∴其对称中心为:(-
+k
,0)(k∈Z);
(4)f(x)min=-2,由2sin(2x+
)=-2,得sin(2x+
)=-1,
∴2x+
=-
+2kπ(k∈Z),
∴x=-
+kπ,k∈Z.
∴f(x)取得最小值时的x的集合为:{x|x=-
+kπ,k∈Z}.
| 3 |
| 4 |
| 2π |
| ω |
| 2π |
| 3 |
| π |
| 12 |
| 3π |
| 4 |
∴ω=2,
又-
| π |
| 12 |
∴φ=2kπ+
| π |
| 6 |
又|φ|<
| π |
| 2 |
∴φ=
| π |
| 6 |
∴f(x)=2sin(2x+
| π |
| 6 |
(2)由-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |

∴f(x)的单调增区间为[kπ-
| π |
| 3 |
| π |
| 6 |
(3)由2x+
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
∴其对称轴方程为:x=
| π |
| 6 |
| π |
| 2 |
由2x+
| π |
| 6 |
| kπ |
| 2 |
| π |
| 12 |
∴其对称中心为:(-
| π |
| 12 |
| π |
| 2 |
(4)f(x)min=-2,由2sin(2x+
| π |
| 6 |
| π |
| 6 |
∴2x+
| π |
| 6 |
| π |
| 2 |
∴x=-
| π |
| 3 |
∴f(x)取得最小值时的x的集合为:{x|x=-
| π |
| 3 |
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,着重考查正弦函数的单调性、对称性、周期性及最值,属于中档题.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目