题目内容
在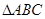 中,已知
中,已知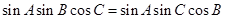
 ,若
,若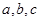 分别是角
分别是角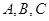 所对的边,则
所对的边,则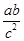 的最大值为 .
的最大值为 .

解析试题分析:根据正弦、余弦定理化简已知条件,然后利用基本不等式即可求出所求式子的最大值.解:在三角形中,由正、余弦定理可将原式转化为: 化简得:3c2=a2+b2≥2ab,故
化简得:3c2=a2+b2≥2ab,故 ,故可知答案为
,故可知答案为
考点:正弦、余弦定理
点评:此题考查学生灵活运用正弦、余弦定理化简求值,会利用基本不等式求函数的最值,是一道综合题.

练习册系列答案
相关题目
题目内容
在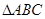 中,已知
中,已知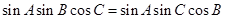
 ,若
,若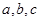 分别是角
分别是角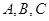 所对的边,则
所对的边,则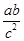 的最大值为 .
的最大值为 .

解析试题分析:根据正弦、余弦定理化简已知条件,然后利用基本不等式即可求出所求式子的最大值.解:在三角形中,由正、余弦定理可将原式转化为: 化简得:3c2=a2+b2≥2ab,故
化简得:3c2=a2+b2≥2ab,故 ,故可知答案为
,故可知答案为
考点:正弦、余弦定理
点评:此题考查学生灵活运用正弦、余弦定理化简求值,会利用基本不等式求函数的最值,是一道综合题.
