Question

（08年绵阳市诊断三文） 已知函数图象上斜率为3的两条切线间的距离为，f(x)的导数为，函数。

（1）若函数g(x)在x=1有极值，求g(x)的解析式；

（2）若函数g(x)在[-1,1]是增函数，且在[-1,1]上都成立，求实数m的取值范围。

Answer 1

解析：，

∴由有，

即切点坐标为(a,a),(-a,-a)，

∴切线方程为y-a=3(x-a)，或y+a=3(x+a)，

整理得3x-y-2a=0，或3x-y+2a=0。

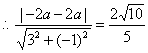解得：，

，

。

（1）

在x=1处有极值，

，即，

解得b=1，

。

（2）∵函数g(x)在[-1,1]是增函数，

在[-1,1]上恒大于0，

。……9分

又在[-1,1]上恒成立，

，

即，

在上恒成立，

，

的取值范围是。