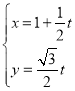题目内容
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为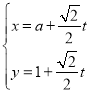 (
(![]() 为参数,
为参数,![]() ).以
).以![]() 为极点,
为极点,![]() 轴非负半轴为极轴,建立极坐标系,曲线
轴非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知曲线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
【答案】(1)曲线![]() 普通方程
普通方程![]() ,曲线
,曲线![]() 的直角坐标方程
的直角坐标方程![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)将![]() 代入
代入![]() 得
得![]() 的普通方程;
的普通方程;
将![]() 左右同时乘以
左右同时乘以![]() 得
得![]() ,再化简得到曲线
,再化简得到曲线![]() 的直角坐标方程。
的直角坐标方程。
(2)将 代入
代入![]() ,得
,得![]() ,利用韦达定理与参数的几何意义可求出实数
,利用韦达定理与参数的几何意义可求出实数![]() 的值。
的值。
(1)曲线![]() 参数方程为
参数方程为 ,
,
则其普通方程![]() ,
,
因为曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,
所以![]() ,
,
即![]() ,即曲线
,即曲线![]() 的直角坐标方程
的直角坐标方程![]() .
.
(2)设![]() 两点所对应参数分别为
两点所对应参数分别为![]() ,
,![]() ,
,
将 代入
代入![]() ,得
,得![]() ,
,
要使![]() 与
与![]() 有两个不同的交点,
有两个不同的交点,
则![]() ,即
,即![]() ,
,
由韦达定理有 ,根据参数的几何意义可知
,根据参数的几何意义可知![]() ,
,![]() ,
,
又由![]() 可得
可得![]() ,即
,即![]() 或
或![]() ,
,
∴当![]() 时,有
时,有
![]() ,符合题意.
,符合题意.
当![]() 时,有
时,有
![]() ,符合题意.
,符合题意.
综上所述,实数![]() 的值为
的值为![]() 或
或![]() .
.

【题目】每年10月中上旬是小麦的最佳种植时间,但小麦的发芽会受到土壤、气候等多方面因素的影响.某科技小组为了解昼夜温差的大小与小麦发芽的多少之间的关系,在不同的温差下统计了100颗小麦种子的发芽数,得到了如下数据:
温差 | 8 | 10 | 11 | 12 | 13 |
发芽数 | 79 | 81 | 85 | 86 | 90 |
(1)请根据统计的最后三组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若由(1)中的线性回归方程得到的估计值与前两组数据的实际值误差均不超过两颗,则认为线性回归方程是可靠的,试判断(1)中得到的线性回归方程是否可靠;
(3)若100颗小麦种子的发芽率为![]() 颗,则记为
颗,则记为![]() 的发芽率,当发芽率为
的发芽率,当发芽率为![]() 时,平均每亩地的收益为
时,平均每亩地的收益为![]() 元,某农场有土地10万亩,小麦种植期间昼夜温差大约为
元,某农场有土地10万亩,小麦种植期间昼夜温差大约为![]() ,根据(1)中得到的线性回归方程估计该农场种植小麦所获得的收益.
,根据(1)中得到的线性回归方程估计该农场种植小麦所获得的收益.
附:在线性回归方程![]() 中,
中,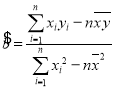 .
.
【题目】某仪器经过检验合格才能出厂,初检合格率为![]() :若初检不合格,则需要进行调试,经调试后再次对其进行检验;若仍不合格,作为废品处理,再检合格率为
:若初检不合格,则需要进行调试,经调试后再次对其进行检验;若仍不合格,作为废品处理,再检合格率为![]() .每台仪器各项费用如表:
.每台仪器各项费用如表:
项目 | 生产成本 | 检验费/次 | 调试费 | 出厂价 |
金额(元) | 1000 | 100 | 200 | 3000 |
(Ⅰ)求每台仪器能出厂的概率;
(Ⅱ)求生产一台仪器所获得的利润为1600元的概率(注:利润![]() 出厂价
出厂价![]() 生产成本
生产成本![]() 检验费
检验费![]() 调试费);
调试费);
(Ⅲ)假设每台仪器是否合格相互独立,记![]() 为生产两台仪器所获得的利润,求
为生产两台仪器所获得的利润,求![]() 的分布列和数学期望.
的分布列和数学期望.