题目内容

12．已知函数f（x）=|x-1|-1，且关于x方程f2（x）+af（x）-2=0有且只有三个实数根，则实数a的值为（　　）
A．1B．-1C．0D．2

分析 作出f（x）=|x-1|-1的图象，令t=f（x），对于方程t2+at-2=0，有一个根为-1，即可得出结论．

解答 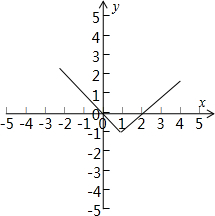解：作出f（x）=|x-1|-1的图象，令t=f（x），对于方程t2+at-2=0的两个根t1=-1，t2∈（-1，+∞），
代入可得a=-1，检验得三个实数根为1，-2，4，满足题意，
故选：B．

点评 本题考查了方程的根与函数的图象的关系，同时考查了学生的作图能力，属于中档题．

练习册系列答案
相关题目
2．已知数列{an}的首项a1=$\frac{1}{2}$，前n项和为Sn，且Sn=p-an．
（Ⅰ）求P及{an}的通项公式；
（Ⅱ）对n∈N*，在an与an+1之间插入3n的数，使得这3n+2项成等差数列，记插入的3n个数之和为bn，令cn=$\frac{4}{3}$nbn，求{cn}的前n项和Tn．
3．已知函数f（x）=$\left\{\begin{array}{l}{\sqrt{x}，0＜x≤4}\\{|x-6|，x＞4}\end{array}\right.$，若方程f（x）=kx+1有三个不同的实数根，则实数k的取值范围是（　　）
A．（-$\frac{1}{6}$，$\frac{1}{4}$）B．（-∞，-$\frac{1}{6}$）∪（$\frac{1}{4}$，+∞）C．[-$\frac{1}{6}$，$\frac{1}{4}$）D．（-$\frac{1}{6}$，$\frac{1}{4}$]
20．已知函数f（x）是定义在（0，+∞）上的可导函数，且f（x）＞0，f（x）+f′（x）＜0
（Ⅰ）讨论函数F（x）=exf（x）的单调性并判断ee-2f（e）＜f（2）是否成立？
（Ⅱ）设0＜x＜1，比较xf（x）与$\frac{1}{x}$f（$\frac{1}{x}$）的大小．
7．已知函数f（x）=|x+a|+|x+$\frac{1}{a}$|（a＞0）
（I）当a=2时，求不等式 f（x）＞3的解集；（Ⅱ）证明：f（m）+$f（-\frac{1}{m}）≥4$．
17．在△ABC中，内角A，B，C所对的边分别为a，b，c，且asinA+bsinB-csinC=bsinA．
（Ⅰ）求∠C的度数；
（Ⅱ）若c=2，求AB边上的高CD的最大值．
4．已知圆C：x2+y2-6y+8=0，若直线y=kx与圆C相切，且切点在第二象限，则实数k=-2$\sqrt{2}$．
1．在（1，+∞）上的函数f（x）满足：①f（2x）=cf（x）（c为正常数）；②当2≤x≤4时，f（x）=1-（x-3）2．若f（x）图象上所有极大值对应的点均落在同一条直线上．则c=（　　）
A．1或$\frac{1}{2}$B．$\frac{1}{2}或2$C．1或3D．1或2
2．已知函数f（x）=lnx-ax+$\frac{a}{x}$，其中a为常数．
（Ⅰ）若f（x）的图象在x=1处的切线经过点（3，4），求a的值；
（Ⅱ）若0＜a＜1，求证：$f（\;\frac{a^2}{2}\;）＞0$；
（Ⅲ）当函数f（x）存在三个不同的零点时，求a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网