题目内容
12.解关于x的不等式:$\sqrt{{x}^{2}+1}$-ax≤1(a>0).分析 原不等式等价于$\left\{\begin{array}{l}{x≥0}\\{(1-{a}^{2}){x}^{2}-2ax≤0}\end{array}\right.$,分类讨论解不等式组可得.
解答 解:原不等式可化为$\sqrt{{x}^{2}+1}$≤1+ax,
等价于$\left\{\begin{array}{l}{1+ax≥1}\\{{x}^{2}+1≤(1+ax)^{2}}\end{array}\right.$,
化简可得$\left\{\begin{array}{l}{x≥0}\\{(1-{a}^{2}){x}^{2}-2ax≤0}\end{array}\right.$,
当1-a2=0即a=1时,解不等式组可得{x|x≥0};
当1-a2>0即0<a<1时,解不等式组可得{x|0≤x≤$\frac{2a}{1-{a}^{2}}$};
当1-a2<0即a>1时,解不等式组可得{x|x≥0}.
点评 本题考查无理不等式的解集,等价转化并分类讨论是解决问题的关键,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.函数y=$\frac{4}{x}$-x的零点是( )
| A. | 2 | B. | -2 | C. | 2,-2 | D. | (2,-2) |
 .
.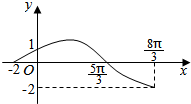 已知函数y=$\left\{\begin{array}{l}{kx+1(-2≤x<0)}\\{2sin(wx+φ)(0≤x≤\frac{8π}{3})}\end{array}\right.$的图象如图所示,试求k,ω,φ的值.
已知函数y=$\left\{\begin{array}{l}{kx+1(-2≤x<0)}\\{2sin(wx+φ)(0≤x≤\frac{8π}{3})}\end{array}\right.$的图象如图所示,试求k,ω,φ的值.