题目内容

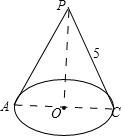
如图，小明想用图中所示的扇形纸片围成一个圆锥，已知扇形的半径为5cm，弧长是6πcm，那么围成的圆锥的体积是

12π

cm³．

分析：利用圆锥的底面圆周长等于扇形的弧长可求出半径，再利用轴截面及勾股定理即可求出圆锥的高，进而计算出体积．

解答：解：如图所示圆锥，设此圆锥的底面圆心为O，半径为r，由题意得2πr=6π，∴r=3．
在Rt△PAO中，由勾股定理得PO=

52-32

=4，
∴V_圆锥=

×π×32×4=12π（cm³）．
故答案为12π．

点评：此题考查了用扇形纸片围成一个圆锥并计算其体积，利用已知条件画出图形及理解圆锥的体积公式是解决问题的关键．

练习册系列答案

小学语文阅读课堂系列答案

相关题目

如图，小明想用图中所示的扇形纸片围成一个圆锥，已知扇形的半径为5 cm，弧长是6πcm，那么围成的圆锥的体积是________cm³．

小明家中有两种酒杯，一种酒杯的轴截面是等腰直角三角形，称之为直角酒杯(如图1)，另一种酒杯的轴截面近似一条抛物线，杯口宽4 cm，杯深为8 cm(如图2)，称之为抛物线酒杯．

(1)请选择适当的坐标系，求出抛物线酒杯的方程．

(2)一次，小明在游戏中注意到一个现象，若将一些大小不等的玻璃球依次放入直角酒杯中，则任何玻璃球能触及酒杯杯底．但若将这些玻璃球放入抛物线酒杯中，则有些小玻璃不能触及酒杯杯底．小明想用所学过数学知识研究一下，当玻璃球的半径r为多大值时，玻璃球一定会触及酒杯杯底部．你能帮助小明解决这个问题吗？

(3)在抛物线酒杯中，放入一根粗细均匀，长度为2 cm的细棒，假设细棒的端点与酒杯壁之间的摩擦可以忽略不计，那么当细棒最后达到平衡状态时，细棒在酒杯中位置如何？

小明家中有两种酒杯，一种酒杯的轴截面是等腰直角三角形，称之为直角酒杯(如图(1))，另一种酒杯的轴截面近似一条抛物线，杯口宽4 cm，杯深为8 cm(如图(2))，称之为抛物线酒杯．

(1)请选择适当的坐标系，求出抛物线酒杯的方程．

(2)一次，小明在游戏中注意到一个现象，若将一些大小不等的玻璃球依次放入直角酒杯中，则任何玻璃球能触及酒杯杯底．但若将这些玻璃球放入抛物线酒杯中，则有些小玻璃球能触及酒杯杯底．小明想用所学过的数学知识研究一下，当玻璃球的半径r为多大值时，玻璃球一定会触及酒杯杯底部．你能帮助小明解决这个问题吗？

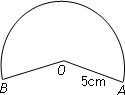
如图，小明想用图中所示的扇形纸片围成一个圆锥，已知扇形的半径为5cm，弧长是6πcm，那么围成的圆锥的体积是________cm³．

如图，小明想用图中所示的扇形纸片围成一个圆锥，已知扇形的半径为5cm，弧长是6πcm，那么围成的圆锥的体积是________cm3．