题目内容
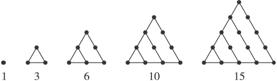
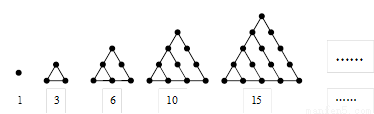
在古希腊,毕达哥拉斯学派把1,3,6,10,15,21,28,…这些数叫做三角形数,因为这些数对应的点可以排成一个正三角形,则第n个三角形数为( )


| A、n | ||
B、
| ||
| C、n2-1 | ||
D、
|
分析:通过观察前几个图形中顶点的个数得,每一个图形中的顶点的个数都可以看成是一个等差数列的前几项的和,再利用等差数列的求和公式即可解决问题.
解答:解:从斜的方向看,根据规律性知:
由1+2+3+…+n
=
n(n+1)可得.
故选:B
由1+2+3+…+n
=
| 1 |
| 2 |
故选:B
点评:本题主要考查了归纳推理,以及数列递推式,属于基础题.所谓归纳推理,就是从个别性知识推出一般性结论的推理.

练习册系列答案
 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案
相关题目
在古希腊,毕达哥拉斯学派把1,3,6,10,15,21,28,…这些数叫做三角形数,这是因为这些数目的点可以排成一个正三角形(如图).
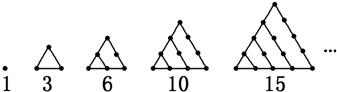
试问三角形数的一般表达式为( )

试问三角形数的一般表达式为( )
| A、n | ||
B、
| ||
| C、n2-1 | ||
D、
|