题目内容
(本题满分12分)
设数列{an}的前n项和为Sn=2n2,{bn}为等比数列,且a1=b1,b2(a2-a1)=b1.
(1)求数列{an}和{bn}的通项公式;
(2)设cn=,求数列{cn}的前n项和Tn.
设数列{an}的前n项和为Sn=2n2,{bn}为等比数列,且a1=b1,b2(a2-a1)=b1.
(1)求数列{an}和{bn}的通项公式;
(2)设cn=,求数列{cn}的前n项和Tn.
解:(1)当n≥2时,
an=Sn-Sn-1=2n2-2(n-1)2=4n-2,当n=1时,a1=S1=2满足上式,
故{an}的通项式为an=4n-2.设{bn}的公比为q,由已知条件b2(a2-a1)=b1知,b1=2,b2=,所以q=,∴bn=b1qn-1=2×,即bn= .
 …….6分
…….6分(2)∵cn===(2n-1)4n-1,∴Tn=c1+c2+…+cn=[1+3×41+5×42+…+(2n-1)4n-1]
4Tn=[1×4+3×42+5×42+…+(2n-3)4n-1+(2n-1)4n]两式相减得:
3Tn=-1-2(41+42+43+…+4n-1)+(2n-1)4n=[(6n-5)4n+5]
∴Tn=[(6n-5)4n+5] . …….12分
略

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
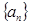 的前
的前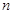 项和为
项和为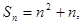
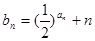 ,求数列
,求数列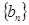 的前
的前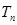 。
。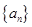 的前n项和
的前n项和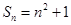 ,则
,则 =
=
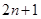


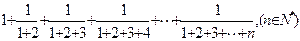
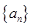 是公差为2的等差数列,且
是公差为2的等差数列,且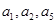 成等比数列,则
成等比数列,则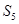 为( )
为( )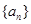 中,若
中,若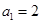 ,且对任意的正整数
,且对任意的正整数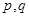 都有
都有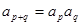 ,
,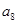 的值为 .
的值为 . 对任意的正整数n,都有
对任意的正整数n,都有 (d为常数),则称
(d为常数),则称 ,“绝对公和”
,“绝对公和” ,则其前2010项和
,则其前2010项和 的最小值为
的最小值为