题目内容
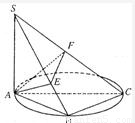 如图已知点B在以AC为直径的圆上,SA⊥面ABC,AE⊥SB于E,AF⊥SC于F.
如图已知点B在以AC为直径的圆上,SA⊥面ABC,AE⊥SB于E,AF⊥SC于F.(1)证明:SC⊥EF;
(2)若SA=a,∠ASC=
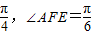 ,求三棱锥S-AEF的体积.
,求三棱锥S-AEF的体积.
【答案】分析:(1)先由AC为圆的直径,点B在圆上⇒BC⊥AC.再利用SA⊥平面ABC,BC?平面ABC⇒AE⊥BC,通过线面垂直的判定定理即可证明AE⊥面SBC,从而有AE⊥SC,通过线面垂直的判定定理即可证明SC⊥面AEF,从而证明结论;(2)由(1)知AE⊥面SBC, ,求出
,求出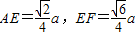 ,进而求得三角形△AEF的面积
,进而求得三角形△AEF的面积
根据已知条件求得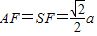 ,进而求得三棱锥S-AEF的体积.
,进而求得三棱锥S-AEF的体积.
解答: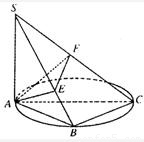 解:(1)证明:
解:(1)证明: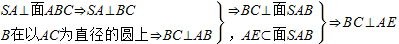 .
. .
.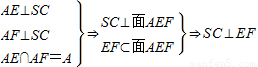 .(6分)
.(6分)
(2)解:Rt△SAC中,∵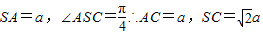
又AF⊥SC,∴F为SC的中点,∴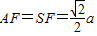 (8分)
(8分)
由(1)知AE⊥面SBC,∴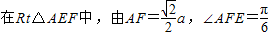
得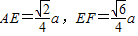 ,∴
,∴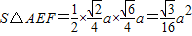 (10分)
(10分)
由(1)知SC⊥面AEF,
∴ (12分)
(12分)
点评:此题是个中档题.考查线面垂直的判定定理和性质定理以及棱锥的体积等基础知识,同时考查空间想象能力、运算能力和推理论证能力.
 ,求出
,求出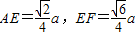 ,进而求得三角形△AEF的面积
,进而求得三角形△AEF的面积根据已知条件求得
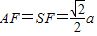 ,进而求得三棱锥S-AEF的体积.
,进而求得三棱锥S-AEF的体积.解答:
 解:(1)证明:
解:(1)证明: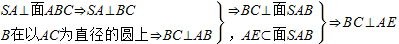 .
. .
.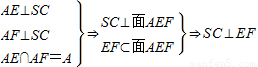 .(6分)
.(6分)(2)解:Rt△SAC中,∵
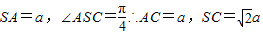
又AF⊥SC,∴F为SC的中点,∴
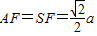 (8分)
(8分)由(1)知AE⊥面SBC,∴
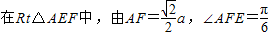
得
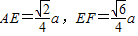 ,∴
,∴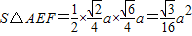 (10分)
(10分)由(1)知SC⊥面AEF,
∴
 (12分)
(12分)点评:此题是个中档题.考查线面垂直的判定定理和性质定理以及棱锥的体积等基础知识,同时考查空间想象能力、运算能力和推理论证能力.

练习册系列答案
相关题目
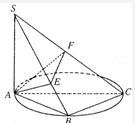 如图已知点B在以AC为直径的圆上,SA⊥面ABC,AE⊥SB于E,AF⊥SC于F.
如图已知点B在以AC为直径的圆上,SA⊥面ABC,AE⊥SB于E,AF⊥SC于F.
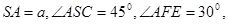 求三棱锥S—AEF的体积.
求三棱锥S—AEF的体积.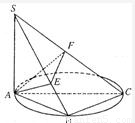 如图已知点B在以AC为直径的圆上,SA⊥面ABC,AE⊥SB于E,AF⊥SC于F.
如图已知点B在以AC为直径的圆上,SA⊥面ABC,AE⊥SB于E,AF⊥SC于F.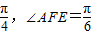 ,求三棱锥S-AEF的体积.
,求三棱锥S-AEF的体积.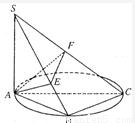 如图已知点B在以AC为直径的圆上,SA⊥面ABC,AE⊥SB于E,AF⊥SC于F.
如图已知点B在以AC为直径的圆上,SA⊥面ABC,AE⊥SB于E,AF⊥SC于F.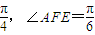 ,求三棱锥S-AEF的体积.
,求三棱锥S-AEF的体积.