题目内容
将半径为2,圆心角为90°的扇形卷成圆锥的侧面,则圆锥的轴截面面积为
.
| ||
| 4 |
| ||
| 4 |
分析:利用扇形的弧长公式求得弧长,除以2π即为圆锥的底面半径,再求圆锥的高,代入轴截面面积公式计算.
解答:解:∵扇形的弧长=
×2=π,
∴圆锥的底面半径为r=π÷2π=
,
∴圆锥的高h=
=
,
∴圆锥的轴截面面积为S=
×2r×h=
×1×
=
.
故答案是:
.
| π |
| 2 |
∴圆锥的底面半径为r=π÷2π=
| 1 |
| 2 |
∴圆锥的高h=
22-
|
| ||
| 2 |
∴圆锥的轴截面面积为S=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
故答案是:
| ||
| 4 |
点评:本题考查了圆锥的轴截面的面积计算及扇形的弧长计算,解题的关键是利用侧面展开图的弧长等于圆锥的底面圆的周长求得底面圆的半径r.

练习册系列答案
相关题目
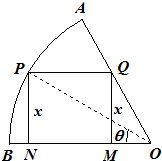 如图,在半径为
如图,在半径为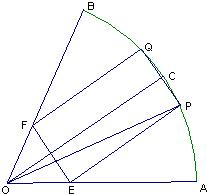 如图,在半径为R、圆心角为
如图,在半径为R、圆心角为 的扇形金属材料中剪出一个长方形EPQF,并且EP与∠AOB的平分线OC平行,设∠POC=θ.
的扇形金属材料中剪出一个长方形EPQF,并且EP与∠AOB的平分线OC平行,设∠POC=θ.
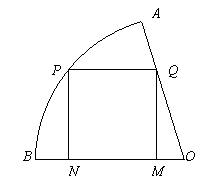 如图,在半径为
如图,在半径为