题目内容
甲、乙两人约定在10点半到12点会面商谈事情,约定先到者应等候另一个人20分钟,即可离去,求两人能会面的概率______(结果用最简分数表示).
由题意知本题是一个几何概型,设事件A为“两人能会面”,
试验包含的所有事件是Ω={(x,y)|10.5<x<12,10.5<y<12},
则事件对应的集合表示的面积是s=
×
=
,
满足条件的事件是A={(x,y)|10.5<x<12,10.5<y<12,|x-y|<
},
所以事件对应的集合表示的面积是
-2×
×[12-(10
+
)][(12-
)-10
]
=
-
×
=
(9-
)=
,
根据几何概型概率公式得到P=
=
.
故答案为:
.

试验包含的所有事件是Ω={(x,y)|10.5<x<12,10.5<y<12},
则事件对应的集合表示的面积是s=
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
| 4 |
满足条件的事件是A={(x,y)|10.5<x<12,10.5<y<12,|x-y|<
| 20 |
| 90 |
所以事件对应的集合表示的面积是
| 9 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 9 |
| 2 |
| 9 |
| 1 |
| 2 |
=
| 9 |
| 4 |
| 23 |
| 2×9 |
| 23 |
| 2×9 |
| 1 |
| 4 |
| 232 |
| 81 |
| 50 |
| 81 |
根据几何概型概率公式得到P=
| ||
|
| 200 |
| 729 |
故答案为:
| 200 |
| 729 |


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
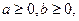 且当
且当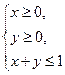 时,恒有
时,恒有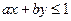 ,则以a,b为坐标的点P(a,b)所形成的平面区域的面积是
,则以a,b为坐标的点P(a,b)所形成的平面区域的面积是






