题目内容
已知f（x）=
，其中a，b为常数，且ab≠2．若f（x）•f（
）=k为常数，则k的值为 ．
| bx+1 |
| 2x+a |
| 1 |
| x |
分析：根据题意分别得到f（x）和f（
）的解析式，算出f（x）•f（
）化简后等于k，根据合分比性质得到k即可；
| 1 |
| x |
| 1 |
| x |
解答：解：由题可知：f（x）•f（
）=
•
=
=k
则根据合分比性质得：
=
=
=
=k，
即k=
；
故答案为：
| 1 |
| x |
| bx+1 |
| 2x+a |
| ||
|
| bx2+(b2+1)x+b |
| 2ax2+(a2+4)x+2a |
则根据合分比性质得：
| b |
| 2a |
| b2+1 |
| a2+4 |
| b2 |
| a2 |
| 1 |
| 4 |
即k=
| 1 |
| 4 |
故答案为：
| 1 |
| 4 |
点评：此题考查学生理解函数的定义，以及合分比性质的灵活运用，难度中档．
练习册系列答案
口算题天天练系列答案
相关题目
已知f（x）=bx+1为x的一次函数，b为不等于1的常数，且g（n）=
，设an=g（n）-g（n-1） （n∈N*），则数列{an}是（ ）
|
| A、等差数列 | B、等比数列 |
| C、递增数列 | D、递减数列 |
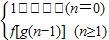，设an=g（n）-g（n-1） （n∈N*），则数列{an}是（ ）
，设an=g（n）-g（n-1） （n∈N*），则数列{an}是（ ）