题目内容
设定义域为[0,1]的函数 同时满足以下三个条件时称
同时满足以下三个条件时称 为“友谊函数”:
为“友谊函数”:
(1)对任意的 ,总有
,总有 ≥0;
≥0;
(2)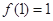 ;
;
(3)若 成立,则下列判断正确的有 .
成立,则下列判断正确的有 .
(1) 为“友谊函数”,则
为“友谊函数”,则 ;
;
(2)函数 在区间[0,1]上是“友谊函数”;
在区间[0,1]上是“友谊函数”;
(3)若 为“友谊函数”,且0≤
为“友谊函数”,且0≤ <
< ≤1,则
≤1,则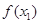 ≤
≤ .
.
【答案】
(1),(2),(3)
【解析】
试题分析:若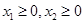 且
且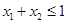 .则有
.则有 成立.令0≤
成立.令0≤ <
< ≤1.则
≤1.则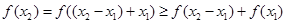
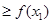 (因为
(因为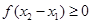 ).所以
).所以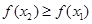 .所以函数f(x)是递增函数所以(3)正确..若
.所以函数f(x)是递增函数所以(3)正确..若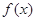 为“友谊函数”则要满足
为“友谊函数”则要满足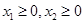 且
且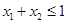 ,则有成立.令
,则有成立.令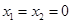 .可得
.可得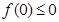 .又因为对任意的
.又因为对任意的 ,总有
,总有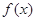 ≥0.所以f(0)=0成立.所以(1)
≥0.所以f(0)=0成立.所以(1)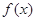 为“友谊函数”,则
为“友谊函数”,则 正确. 函数
正确. 函数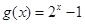 在区间[0,1]上可得f(x)
在区间[0,1]上可得f(x) 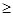 0,f(1)=1成立.又因为
0,f(1)=1成立.又因为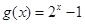 是递增的.所以函数
是递增的.所以函数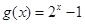 在区间[0,1]上是“友谊函数”正确.
在区间[0,1]上是“友谊函数”正确.
考点:1.函数的单调性.2.新定义的函数的性质.3.夹值法的思想证明相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目