题目内容
【题目】如图,已知抛物线C:![]() (
(![]() )的焦点F到直线
)的焦点F到直线![]() 的距离为
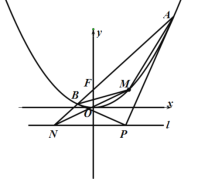
的距离为![]() .AB是过抛物线C焦点F的动弦,O是坐标原点,过A,B两点分别作此抛物线的切线,两切线相交于点P.
.AB是过抛物线C焦点F的动弦,O是坐标原点,过A,B两点分别作此抛物线的切线,两切线相交于点P.
(1)求证:![]() .
.
(2)若动弦AB不经过点![]() ,直线AB与准线l相交于点N,记MA,MB,MN的斜率分别为
,直线AB与准线l相交于点N,记MA,MB,MN的斜率分别为![]() ,
,![]() ,
,![]() .问:是否存在常数λ,使得
.问:是否存在常数λ,使得![]() 在弦AB运动时恒成立?若存在,求λ的值;若不存在,说明理由.
在弦AB运动时恒成立?若存在,求λ的值;若不存在,说明理由.
【答案】(1)见解析 (2)存在,-1
【解析】
(1)根据已知求出抛物线方程,要证![]() ,只需证明
,只需证明![]() ,设
,设![]() ,
,![]() ,利用求导方法求出切线
,利用求导方法求出切线![]() 斜率,设出直线
斜率,设出直线![]() 的方程,与抛物线方程联立,利用根与系数关系,即可得证;
的方程,与抛物线方程联立,利用根与系数关系,即可得证;
(2)设直线![]() ,求出
,求出![]() 点坐标,求出
点坐标,求出![]() ,利用
,利用![]() 关系,
关系,![]() 用
用![]() 表示,代入
表示,代入![]() ,判断是否存在
,判断是否存在![]() 使得
使得![]() 时等式均成立,即可得出结论.
时等式均成立,即可得出结论.
(1)![]() (
(![]() )
)![]()
由已知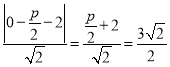 ,
,
![]()
故抛物线方程为![]()
![]() 依题意,设直线AB方程为
依题意,设直线AB方程为![]() (
(![]() )
)
联立![]() 得:
得:![]()
设![]() ,
,![]()
![]() ,
,![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
(2)将![]() 代入
代入![]() 得
得![]()
![]()
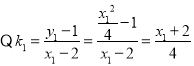 ,
,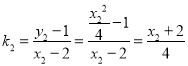
![]()
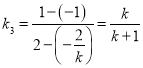 .
.
若有![]() 成立,则有
成立,则有
整理得![]() 恒成立,
恒成立,![]() .
.
故存在![]()
![]() 成立.
成立.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】为了增强消防意识,某部门从男,女职工中各随机抽取了20人参加消防知识测试(满分为100分),这40名职工测试成绩的茎叶图如下图所示

(1)根据茎叶图判断男职工和女职工中,哪类职工的测试成绩更好?并说明理由;
(2)(ⅰ)求这40名职工成绩的中位数![]() ,并填写下面列联表:
,并填写下面列联表:
超过 | 不超过 | |
男职工 | ||
女职工 |
(ⅱ)如果规定职工成绩不少于m定为优秀,根据(ⅰ)中的列联表,能否有99%的把握认为消防知识是否优秀与性别有关?
附: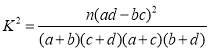 .
.
P( | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |