题目内容
已知两曲线y=x3+ax和y=x2+bx+c都经过点P(1,2),且在点P处有公切线,则当 x≥
时,logb
的最小值为( )
| 1 |
| 2 |
| ax2-c |
| x |
| A、-1 | ||
| B、1 | ||
| C、2 | ||
D、
|
分析:先由曲线y=x3+ax经过点P(1,2),求得a值,进而利用导数的几何意义求得曲线y=x3+ax经过点P(1,2)的切线方程l;再由y=x2+bx+c经过点P(1,2)的切线方程也是l,可求得b、c的值;最后代入logb
,利用均值定理求最小值即可
| ax2-c |
| x |
解答:解:将P(1,2)代入两曲线y=x3+ax和y=x2+bx+c,得
设f(x)=x3+x,g(x)=x2+bx+c
∵f′(x)=3x2+1,∴f′(1)=4∵g′(x)=2x+b,∴g′(1)=2+b
∵两曲线在点P处有公切线
∴f′(1)=g′(1)=2+b=4,
∴b=2,c=-1
∴logb
=log2
=log2(x+
)≥log22=1 (当且仅当x=1时取等号)
故选B
|
设f(x)=x3+x,g(x)=x2+bx+c
∵f′(x)=3x2+1,∴f′(1)=4∵g′(x)=2x+b,∴g′(1)=2+b
∵两曲线在点P处有公切线
∴f′(1)=g′(1)=2+b=4,
∴b=2,c=-1
∴logb
| ax2-c |
| x |
| x2+1 |
| x |
| 1 |
| x |
故选B
点评:本题考查了导数的几何意义和均值定理的运用,解题时要抓住要害,准确作答.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案
相关题目
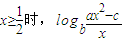 的最小值为( )
的最小值为( )