题目内容
(本题满分12分)
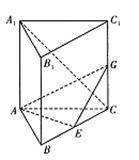
如图,在直三棱柱ABC-A1B1C1中,![]() E是BC的中点。
E是BC的中点。
(1)求异面直线AE与A1C所成的角;
(2)若G为C1C上一点,且EG⊥A1C,试确定点G的位置;
|
解:(1)取B![]() 1C1的中点E1,连A1E1,E1C,则AE∥A1E1,∴∠E1A1C是异面直线A
1C1的中点E1,连A1E1,E1C,则AE∥A1E1,∴∠E1A1C是异面直线A
与A1C所成的角。设![]() ,则
,则![]()
![]()
![]()
![]() 中,
中, ![]() 。
。
|
![]() (2).由(1)知,A1E1⊥B1C1,
(2).由(1)知,A1E1⊥B1C1,
又因为三棱柱ABC-A1B1C1是直三棱柱
![]()
![]() ⊥BCC1B1,又
⊥BCC1B1,又![]() EG⊥A1C
EG⊥A1C ![]() CE1⊥EG.
CE1⊥EG.
![]() ∠
∠![]() =∠GEC
=∠GEC ![]()
![]() ~
~![]()
![]() 即
即![]() 得
得![]()
所以G是CC1的中点 -------![]() --------------------- --8分
--------------------- --8分
(3)连结AG,设P是AC的中点,过点P作PQ⊥AG于Q,连EP,EQ,则EP⊥AC.
又![]() 平面ABC⊥平面ACC1A1
平面ABC⊥平面ACC1A1 ![]() EP⊥平面ACC1A1
EP⊥平面ACC1A1
而PQ⊥AG ![]() EQ⊥AG.
EQ⊥AG.![]() ∠PQE是二面角C-AG-E的平面角.
∠PQE是二面角C-AG-E的平面角.
由EP=a,AP=a,PQ=![]() ,得
,得![]()
所以二面角C-AG-E的平面角是![]() ,而所求二面角
,而所求二面角![]() 是二面角C-AG-E的补角,故二面角
是二面角C-AG-E的补角,故二面角![]() 的平面角是
的平面角是![]() -------
-------![]() -----------12分
-----------12分
解析:
略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 <1,xÎR }.
<1,xÎR }. ,求实数a的取值范围.
,求实数a的取值范围. (
( ,
, 为常数),且方程
为常数),且方程 有两个实根为
有两个实根为 .
. 的解析式;
的解析式; 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
 ⊥平面
⊥平面
 的大小;
的大小; 到平面
到平面