题目内容
已知曲线C1: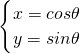 (θ为参数)和曲线C2=:x2+y2-2
(θ为参数)和曲线C2=:x2+y2-2 x+2y+3=0義于直线l1对称,直线l2过原点且与l1的夹角为30°,则直线l2的方程为
x+2y+3=0義于直线l1对称,直线l2过原点且与l1的夹角为30°,则直线l2的方程为
- A.y=
 x
x - B.x=0或y=
 x
x - C.y=
 x
x - D.x=0或y=
 x
x
B
分析:利用两圆的方程相减,求出两等圆的对称轴直线l1的方程,再设所求直线的斜率为k,代入两条直线的夹角公式求出夹角的正确的值,列出关于k的方程即可得到k的值.
解答:曲线C1: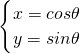 (θ为参数)化成普通方程为:x2+y2-1=0,
(θ为参数)化成普通方程为:x2+y2-1=0,
又曲线C2:x2+y2-2 x+2y+3=0,
x+2y+3=0,
两方程相减得直线l1: x-y-2=0,
x-y-2=0,
设直线l1,l2的斜率分别为 k1,k2,l1与l2的夹角为θ=30°,
则∴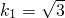 .
.
则tan30°=|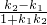 |,
|,
即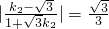 ,
,
∴k= .
.
另外,当直线l2的斜率不存在时,即l2的方程为:x=0也符合要求,
则直线l2的方程为:x=0或y= x.
x.
故选B.
点评:本题考查参数方程化成普通方程,两条直线的夹角公式,根据三角函数的值求角,求出两圆的对称轴是解题的关键.
分析:利用两圆的方程相减,求出两等圆的对称轴直线l1的方程,再设所求直线的斜率为k,代入两条直线的夹角公式求出夹角的正确的值,列出关于k的方程即可得到k的值.
解答:曲线C1:
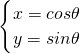 (θ为参数)化成普通方程为:x2+y2-1=0,
(θ为参数)化成普通方程为:x2+y2-1=0,又曲线C2:x2+y2-2
 x+2y+3=0,
x+2y+3=0,两方程相减得直线l1:
 x-y-2=0,
x-y-2=0,设直线l1,l2的斜率分别为 k1,k2,l1与l2的夹角为θ=30°,
则∴
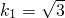 .
.则tan30°=|
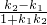 |,
|,即
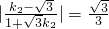 ,
,∴k=
 .
.另外,当直线l2的斜率不存在时,即l2的方程为:x=0也符合要求,
则直线l2的方程为:x=0或y=
 x.
x.故选B.
点评:本题考查参数方程化成普通方程,两条直线的夹角公式,根据三角函数的值求角,求出两圆的对称轴是解题的关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目