题目内容
4.已知向量:$\overrightarrow{a}$,$\overrightarrow{b}$满足2$\overrightarrow{a}$+$\overrightarrow{b}$=(-1,-4,3),$\overrightarrow{a}$-2$\overrightarrow{b}$=(2,4,-5),求$\overrightarrow{a}$,$\overrightarrow{b}$.分析 由已知条件利用向量的坐标运算能求出$\overrightarrow{a}$,$\overrightarrow{b}$.
解答 解:∵向量:$\overrightarrow{a}$,$\overrightarrow{b}$满足2$\overrightarrow{a}$+$\overrightarrow{b}$=(-1,-4,3),①
$\overrightarrow{a}$-2$\overrightarrow{b}$=(2,4,-5),②
∴①×2,得4$\overrightarrow{a}$+2$\overrightarrow{b}$=(-2,-8,6),③
∴②+③,得$5\overrightarrow{a}$=(0,-4,1),
解得$\overrightarrow{a}$=(0,-$\frac{4}{5}$,$\frac{1}{5}$).
∴$\overrightarrow{b}$=(-1,-4,3)-$2\overrightarrow{a}$=(-1,-4,3)-(0,-$\frac{8}{5}$,$\frac{2}{5}$)=(-1,-$\frac{12}{5}$,$\frac{13}{5}$).
点评 本题考查向量的求法,是基础题,解题时要认真审题,注意向量的坐标运算的性质的合理运用.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
14.在四面体S-ABC中,SA=8,SB=10,SC=AB=BC=CA=6,A′,B′,C′分别是棱SA,SB,SC上的点,且SA′=2,SB′=2.5,SC′=4,则截面A′B′C′将四面体S-ABC分成的两部分体积之比为( )
| A. | $\frac{1}{24}$ | B. | $\frac{1}{23}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{8}$ |
15.求值:
(1)cos$\frac{π}{5}$cos$\frac{2π}{5}$;
(2)cos$\frac{2π}{7}$•cos$\frac{4π}{7}$•cos$\frac{6π}{7}$.
(1)cos$\frac{π}{5}$cos$\frac{2π}{5}$;
(2)cos$\frac{2π}{7}$•cos$\frac{4π}{7}$•cos$\frac{6π}{7}$.
12.函数y=cos($\frac{π}{2}$-x),x∈[-π,$\frac{π}{2}$]的单调性是( )
| A. | 在[-π,-$\frac{π}{2}$]上是减函数,在[-$\frac{π}{2}$,$\frac{π}{2}$]上是增函数 | |
| B. | 在[-π,0]上是减函数,在[0,$\frac{π}{2}$]上是增函数 | |
| C. | 在[-π,-$\frac{π}{2}$]上是增函数,在[-$\frac{π}{2}$,$\frac{π}{2}$]上是减函数 | |
| D. | 在[-π,0]上是增函数,在[0,$\frac{π}{2}$]上是减函数 |
19.方程cos($\frac{5}{2}$π+x)=($\frac{1}{2}$)x在区间(0,100π)内解的个数是( )
| A. | 98 | B. | 100 | C. | 102 | D. | 200 |
7.如图给出的是计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{2012}$的值的一个程序框图,则判断框内应填入的条件是( ) 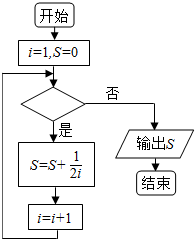

| A. | i≤1 005? | B. | i>1 005? | C. | i≤1 006? | D. | i>1 006? |