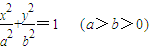题目内容
（1）求焦点坐标为F1（0，-3），F2（0，3）且长轴长为10的椭圆的标准方程；
（2）求经过点（3，-1）的等轴双曲线的标准方程．
（2）求经过点（3，-1）的等轴双曲线的标准方程．
分析：（1）设椭圆C的方程为：
+
=1（a＞b＞0），由题意及a，b，c的平方关系即可求得a，b值；
（2）设出双曲线方程，代入点（3，-1）的坐标，即可求得结论．
| y2 |
| a2 |
| x2 |
| b2 |
（2）设出双曲线方程，代入点（3，-1）的坐标，即可求得结论．
解答：解：（1）设椭圆C的方程为：
+
=1（a＞b＞0），
由题意知，2a=10，c=3，∴a=5，b2=a2-c2=25-9=16，
椭圆C的标准方程为：
+
=1．
（2）由题意，可设所求双曲线的方程为x2-y2=m
∵双曲线经过点（3，-1），代入得m=8
∴所求方程为
-
=1．
| y2 |
| a2 |
| x2 |
| b2 |
由题意知，2a=10，c=3，∴a=5，b2=a2-c2=25-9=16，
椭圆C的标准方程为：
| y2 |
| 25 |
| x2 |
| 16 |
（2）由题意，可设所求双曲线的方程为x2-y2=m
∵双曲线经过点（3，-1），代入得m=8
∴所求方程为
| x2 |
| 8 |
| y2 |
| 8 |
点评：本题考查椭圆、双曲线的标准方程、几何性质，考查学生的计算能力，属于基础题．
练习册系列答案
期末100分闯关海淀考王系列答案
相关题目
已知抛物线C的顶点在原点，焦点坐标为F（2，0），点P的坐标为（m，0）（m≠0），设过点P的直线l交抛物线C于A，B两点，点P关于原点的对称点为点Q．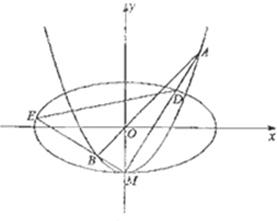
已知椭圆C1：