Question

已知集合A和集合B各含有12个元素，A∩B含有4个元素，试求同时满足下面两个条件的集合C的个数：（1）C?A∪B且C中含有3个元素，（2）C∩A≠φ（φ表示空集）．

Answer 1

【答案】分析：集合韦恩图求出A∪B中元素的个数，再利用排列组合知识求解即可．
解答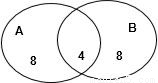：解：因为A、B各含12个元素，A∩B含有4个元素，因此
A∪B元素的个数是12+12-4=20
故满足题目条件（1）的集合的个数是C₂₀³，
在上面集合中，还满足A∩C=φ的集合C的个数是C₈³
因此，所求集合C的个数是C₂₀³-C₈³=1084
点评：本题考查集合中元素的个数、子集个数以及排列组合知识，难度不大．