题目内容
甲、乙两位同学做摸球游戏.游戏规则规定：两人轮流从一个放有2个红球，3个黄球，1个白球的6个小球只有颜色不同的暗箱中取球，每次每人只取一球，每取出一个后立即放回，另一人接着取，取出后也立即放回，谁先取到红球，谁为胜者.现甲先取，(1)求甲取球次数不超过三次就获胜的概率；
(2)求甲获胜的概率.
解：(1)甲第一次取得红球的概率为
，甲第二次取得红球的概率为
×
×
=
(
)1，
甲第三次取得红球的概率为
(
)2，
∴甲取球次数不超过三次就获胜的概率P=
+
×
×
+
×(
)2=
.
(2)甲第一次取得红球的概率为
，甲第二次取得红球的概率为
×
×
=
(
)1，甲第三次取得红球的概率为
(
)2，…，甲第n次取得红球的概率为
(
)n-1.
∴甲获胜的概率P=
［
+
(
)1+
(
)2+…+
(
)n-1］=
=
.
练习册系列答案
世纪百通期末金卷系列答案
相关题目
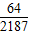，求甲的取球次数．