题目内容
甲、乙两位同学做摸球游戏.游戏规则规定:两人轮流从一个放有2个红球,3个黄球,1个白球的6个小球(只有颜色不同)的暗箱中取球,每次每人只取一球,每取出一个后立即放回,另一人接着取,取出后也立即放回,谁先取到红球,谁为胜者,现甲先取.
(Ⅰ)求甲取球次数不超过二次就获胜的概率.
(Ⅱ)若直到甲第n次取出球时,恰好分出胜负的概率等于
,求甲的取球次数.
(Ⅰ)求甲取球次数不超过二次就获胜的概率.
(Ⅱ)若直到甲第n次取出球时,恰好分出胜负的概率等于
| 64 | 2187 |
分析:(Ⅰ)设“甲取球次数不超过二次就获胜”为事件A,进而计算可得两人每次抽到红球与抽不到红球的概率,分析可得A有两种情况:①甲第一次取球就得红球,②甲第二次取球得红球,由相互独立事件的概率乘法公式,计算可得每种情况的概率,进而由互斥事件概率的加法公式,计算可得答案;
(Ⅱ)若直到甲第n次取出球时,恰好分出胜负,则甲在前n-1抽取中,抽到的都不是红球,同时乙也抽了n-1次,也没有抽到红球,即可得关于n的表达式,解可得答案.
(Ⅱ)若直到甲第n次取出球时,恰好分出胜负,则甲在前n-1抽取中,抽到的都不是红球,同时乙也抽了n-1次,也没有抽到红球,即可得关于n的表达式,解可得答案.
解答:解(Ⅰ)设“甲取球次数不超过二次就获胜”为事件A,
根据题意,两人每次抽到红球的概率都为
=
,则抽不到红球的概率为1-
=
,
则A有两种情况:①甲第一次取球就得红球,其概率P1=
,
②甲第二次取球得红球,其概率P2=
×
×
=
,
则P(A)=P1+P2=
+
=
,
甲取球次数不超过二次就获胜的概率
(Ⅱ)由题意可得:若直到甲第n次取出球时,恰好分出胜负,
则甲在前n-1抽取中,抽到的都不是红球,同时乙也抽了n-1次,也没有抽到红球,
则有(
)n-1•(
)n-1•
=
,
解得n=4
故甲取球次数为4次.
根据题意,两人每次抽到红球的概率都为
| 2 |
| 6 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
则A有两种情况:①甲第一次取球就得红球,其概率P1=
| 1 |
| 3 |
②甲第二次取球得红球,其概率P2=
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 4 |
| 27 |
则P(A)=P1+P2=
| 1 |
| 3 |
| 4 |
| 27 |
| 13 |
| 27 |
甲取球次数不超过二次就获胜的概率
| 13 |
| 27 |
(Ⅱ)由题意可得:若直到甲第n次取出球时,恰好分出胜负,
则甲在前n-1抽取中,抽到的都不是红球,同时乙也抽了n-1次,也没有抽到红球,
则有(
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 64 |
| 2187 |
解得n=4
故甲取球次数为4次.
点评:本题考查相互独立事件的概率的计算,注意(Ⅱ)中,要根据题意,由甲抽取的情况来分析乙的抽取的次数.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
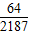 ,求甲的取球次数.
,求甲的取球次数.