题目内容
【题目】在四面体![]() 中,
中, ![]() 分别是
分别是![]() 的中点.则下述结论:
的中点.则下述结论:
①四面体![]() 的体积为
的体积为![]() ;
;
②异面直线![]() 所成角的正弦值为
所成角的正弦值为![]() ;
;
③四面体![]() 外接球的表面积为
外接球的表面积为![]() ;
;
④若用一个与直线![]() 垂直,且与四面体的每个面都相交的平面
垂直,且与四面体的每个面都相交的平面![]() 去截该四面体,由此得到一个多边形截面,则该多边形截面面积最大值为
去截该四面体,由此得到一个多边形截面,则该多边形截面面积最大值为![]() .
.
其中正确的有_____.(填写所有正确结论的编号)
【答案】①③④.
【解析】
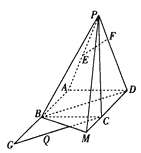
补图成长方体,在长方体中利用割补法求四面体的体积,和外接球的表面积,以及异面直线的夹角,作出截面即可计算截面面积的最值.
根据四面体特征,可以补图成长方体设其边长为![]() ,
,
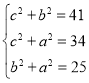 ,解得
,解得![]()
补成长,宽,高分别为![]() 的长方体,在长方体中:
的长方体,在长方体中:
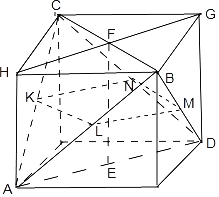
①四面体![]() 的体积为
的体积为![]() ,故正确
,故正确
②异面直线![]() 所成角的正弦值等价于边长为
所成角的正弦值等价于边长为![]() 的矩形的对角线夹角正弦值,可得正弦值为
的矩形的对角线夹角正弦值,可得正弦值为![]() ,故错;
,故错;
③四面体![]() 外接球就是长方体的外接球,半径
外接球就是长方体的外接球,半径![]() ,其表面积为
,其表面积为![]() ,故正确;
,故正确;
④由于![]() ,故截面为平行四边形
,故截面为平行四边形![]() ,可得
,可得![]() ,
,
设异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ,则
,则![]() ,算得
,算得![]() ,
,
![]() .故正确.
.故正确.
故答案为:①③④.

练习册系列答案
相关题目
【题目】函数f(x)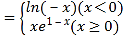 ,若关于x的方程f2(x)﹣af(x)+a﹣a2=0有四个不等的实数根,则a的取值范围是( )
,若关于x的方程f2(x)﹣af(x)+a﹣a2=0有四个不等的实数根,则a的取值范围是( )
A.![]() B.(﹣∞,﹣1)∪[1,+∞)
B.(﹣∞,﹣1)∪[1,+∞)
C.(﹣∞,﹣1)∪{1}D.(﹣1,0)∪{1}